
(本小题满分16分) 若x,y满足 ,求:
,求:
(1)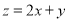 的最小值;
的最小值;
(2)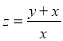 的最大值;
的最大值;
(3)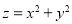 的范围.
的范围.
(1)
(2)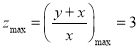
(3)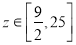
【解析】
试题分析:(1)如果可行域是一个多边形,那么一般在某点处使目标函数取得最大值或最小值,最优解一般就是多边形的某个顶点,特别的,当表示线性目标函数的直线与可行域的某条边平行时,其最优解可能有无数多个;(2)常见代数式的几何意义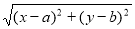 表示点
表示点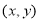 与点
与点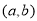 的距离;
的距离; 表示点
表示点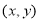 与点
与点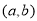 连线的斜率,这些代数式的几何意义能使所求的问题得以转化,往往是解决问题的关键
连线的斜率,这些代数式的几何意义能使所求的问题得以转化,往往是解决问题的关键
试题解析:
如图,
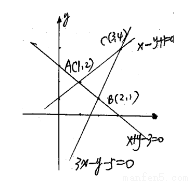
作出满足已知条件的可行域为△ABC内(及边界)区域,其中A(1,2),B(2,1),C(3, 4).
(1)目标函数 ,表示直线
,表示直线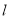 :
: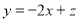 ,
,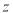 表示该直线纵截距,当
表示该直线纵截距,当 过点A(1,2)时纵截距有最小值,故
过点A(1,2)时纵截距有最小值,故 . 7分
. 7分
(2)目标函数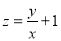 ,记
,记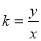 .
.
则k表示区域中的点与坐标原点连线的斜率,当直线过点A时,斜率最大,即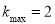 ,即
,即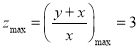 . 11分
. 11分
(3)目标函数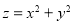 表示区域内的点到坐标系点的距离的平方,又原点O到AB的距离
表示区域内的点到坐标系点的距离的平方,又原点O到AB的距离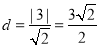 且垂足是D
且垂足是D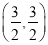 在线段AB上,故
在线段AB上,故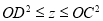 ,
,
即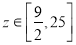 16分
16分
考点:线性规划


科目:高中数学 来源:2014-2015学年江西省高二上学期第一次月考理科数学试卷(解析版) 题型:解答题
(12分)从圆C: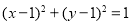 外一点
外一点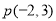 ,向圆C引切线,切点为M、N.
,向圆C引切线,切点为M、N.
(1)求切线方程.
(2)求过二切点的直线方程.
查看答案和解析>>
科目:高中数学 来源:2015届内蒙古赤峰市高二下学期期末理科数学试卷(解析版) 题型:解答题
已知函数f(x)=x2﹣alnx,a∈R.
(Ⅰ)当a=4时,求函数f(x)在[1,e]上的最小值及相应的x的值;
(Ⅱ)若存在x∈[2,e],使得f(x)≥(a﹣2)x成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省高邮市高二九月月考数学试卷(解析版) 题型:填空题
已知某算法的流程图如图所示,若将输出的数组(x,y)依次记为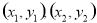 …,
…, ,…,则程序运行结束时输出的最后一个数组为 .
,…,则程序运行结束时输出的最后一个数组为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com