在中.已知..．(Ⅰ)求的值,(Ⅱ)求的值．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

（本小题满分12分）
在中，已知，，．
（Ⅰ）求的值；
（Ⅱ）求的值．

（Ⅰ）
（Ⅱ）

解析

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

在中，角A、B、C的对边分别为a．b．c，且满足，，边上中线的长为．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

（本题满分12分）
在△ABC中，三个内角是A、B、C的对边分别是a、b、c，其中c=10，且
（I）求证：△ABC是直角三角形；
（II）设圆O过A、B、C三点，点P位于劣弧AC上，∠PAB=60°．求四边形ABCP的面积．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

（本小题满分13分）△ABC的外接圆半径为1，角A，B，C的对边分别为a，ｂ，ｃ．向量=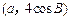, 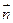=满足//.
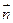（1）求的取值范围；
（2）若实数x满足abx=a+b，试确定x的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

（本小题满分13分）
设的内角的对边分别为，且，,求：
（Ⅰ）的值；
（Ⅱ）的值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

（本小题满分13分）
某港口要将一件重要物品用小艇送到一艘正在航行的轮船上，在小艇出发时，轮船位于港口的O北偏西30°且与该港口相距20海里的A处，并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶，经过t小时与轮船相遇.
（I）若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？
（II）为保证小艇在30分钟内（含30分钟）能与轮船相遇，试确定小艇航行速度的最小值.

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

（12分）△ABC中
（1）求△ABC的面积；
（2）若b+c=6，求a的值。