
(1)设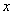 、
、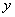 是不全为零的实数,试比较
是不全为零的实数,试比较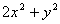 与
与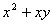 的大小;
的大小;
(2)设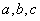 为正数,且
为正数,且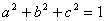 ,求证:
,求证: .
.
(1)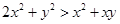 ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)比较两个数的大小,一般是用作差法,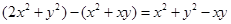 ,下面就是确定
,下面就是确定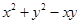 与0的大小,
与0的大小,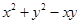 是一个二次三项式,因此我们可用配方法配方,
是一个二次三项式,因此我们可用配方法配方,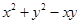
 ,由于
,由于 不全为零,因此
不全为零,因此 ,从而有
,从而有
 ;另外本题实质是比较
;另外本题实质是比较 与
与 的大小,想到基本不等式,有
的大小,想到基本不等式,有 (
( 时取等号),而
时取等号),而 ,再讨论下等号能否成立即可;(2)这是条件不等式的证明,而且已知与求证式都是对称式,因此大胆想象等号成立时,各字母应该相等,事实上也正是在
,再讨论下等号能否成立即可;(2)这是条件不等式的证明,而且已知与求证式都是对称式,因此大胆想象等号成立时,各字母应该相等,事实上也正是在 时取等号,接下来考虑不等式的证明,关键是条件怎么应用,这里我们偿试把
时取等号,接下来考虑不等式的证明,关键是条件怎么应用,这里我们偿试把 中的分子的1全部用
中的分子的1全部用 代换
,有
代换
,有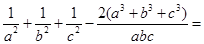
 ,把这个分式展开重新分组为
,把这个分式展开重新分组为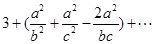
 ,下面易证.
,下面易证.
试题解析:(1)解法1: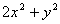 -
- =
= =
=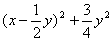 3分
3分
因为 、
、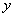 是不全为零的实数,所以
是不全为零的实数,所以 ,即
,即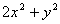 >
> 。 6分
。 6分
解法2:当 时,
时, 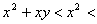
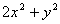 ; 2分
; 2分
当 时,作差:
时,作差:
 ;
;
又因为 、
、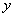 是不全为零的实数,所以当
是不全为零的实数,所以当 时,
时,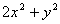 >
> 。
。
综上,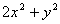 >
> 。
6分
。
6分
(2)证明:当 时,取得等号3。
7分
时,取得等号3。
7分
作差比较:


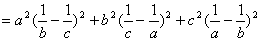
 .
.
所以, 14分
14分
考点:(1)比较两个实数的大小;(2)条件不等式的证明.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| c2 |
| 2(a3+b3+c3) |
| abc |
查看答案和解析>>
科目:高中数学 来源: 题型:044
(1)设二次函数f ( x ) = ax2 + bx + c,证明 f ( x ) > 0对一切x∈R恒成立的充要条件是a > 0,且Δ= b2-4ac < 0;
(2)设a1,a2,…,an,b1,b2,…,bn是不全为零的任意实数,利用(1)的结论证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
(2)设a1,a2,…,an,b1,b2,…,bn是不全为零的任意实数,利用(1)的结论证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com