
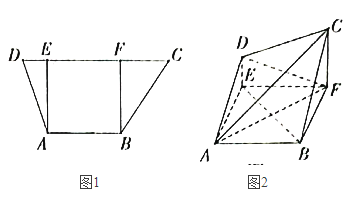
【题目】如图1,在梯形ABCD中,![]() ,
,![]() ,
,![]() ,过A,B分别作CD的垂线,垂足分别为E,F,已知
,过A,B分别作CD的垂线,垂足分别为E,F,已知![]() ,
,![]() ,将梯形ABCD沿AE,BF同侧折起,使得平面
,将梯形ABCD沿AE,BF同侧折起,使得平面![]() 平面ABFE,平面
平面ABFE,平面![]() 平面BCF,得到图2.
平面BCF,得到图2.
(1)证明:![]() 平面ACD;
平面ACD;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析.(2)![]()
【解析】
(1)设![]() ,取AC中点M,连接OM,DM,可证明四边形DEOM为平行四边形 可得
,取AC中点M,连接OM,DM,可证明四边形DEOM为平行四边形 可得![]() ,即得证;
,即得证;
(2)建立如图空间直角坐标系,求解平面ADF,平面ADC的法向量,由二面角的向量公式即得解.
(1)设![]() ,取AC中点M,连接OM,DM
,取AC中点M,连接OM,DM
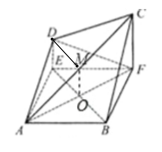
四边形ABFE为正方形 ∴为AF中点 ∵M为AC中点 ∴![]()
∵平面![]() 平面ABFE
平面ABFE
平面![]() 平面
平面![]()
![]()
![]() 平面ABFE
平面ABFE
![]() 平面ADE
平面ADE
又∵平面![]() 平面BCF
平面BCF
∴平面![]() 平面ABFE 同理,
平面ABFE 同理,![]() 平面ABFE
平面ABFE
又∵![]() ,
,![]() ∴
∴![]()
∴![]()
∴四边形DEOM为平行四边形 ∴![]()
∵![]() 平面ADC,
平面ADC,![]() 平面ADC
平面ADC
∴平面ADC
(2)由题意EA,EF,ED两两垂直,以EA为x轴,EF为y轴,ED为z轴建立空间直角坐标系![]()
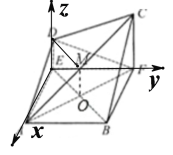
∴![]() ,
,![]() ,
,![]() ,
,![]()
设平面ADF的法向量为![]()
∵![]() ,
,![]()
∴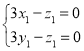
∴![]()
设平面ADC的法向量为![]()
∵![]()
∴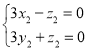
∴![]()
设二面角![]() 的平面角为θ,由图像得θ为锐角,
的平面角为θ,由图像得θ为锐角,
∴![]()


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】2016里约奥运会期间,小赵常看的4个电视频道中有2个频道在转播奥运比赛,若小赵这时打开电视,随机打开其中两个频道试看,那么,小赵所看到的第一个电视台恰好没有转播奥运比赛,而第二个电视台恰好在转播奥运比赛的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(k+![]() )lnx+
)lnx+![]() ,k∈[4,+∞),曲线y=f(x)上总存在两点M(x1,y1),N(x2,y2),使曲线y=f(x)在M,N两点处的切线互相平行,则x1+x2的取值范围为
,k∈[4,+∞),曲线y=f(x)上总存在两点M(x1,y1),N(x2,y2),使曲线y=f(x)在M,N两点处的切线互相平行,则x1+x2的取值范围为
A. (![]() ,+∞) B. (
,+∞) B. (![]() ,+∞) C. [
,+∞) C. [![]() ,+∞) D. [
,+∞) D. [![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐代诗人李欣的是![]() 古从军行
古从军行![]() 开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有缺的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为
开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有缺的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为![]() ,若将军从
,若将军从![]() 出发,河岸线所在直线方程
出发,河岸线所在直线方程![]() ,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)分别求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,交曲线
两点,交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 5 |
| 0 |
(1)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数![]() 的解析式;
的解析式;
(2)将![]() 图象上所有点向左平行移动
图象上所有点向左平行移动![]() 个单位长度,并把图象上所有点的横坐标缩短为原来的
个单位长度,并把图象上所有点的横坐标缩短为原来的![]() (纵坐标不变),得到
(纵坐标不变),得到![]() 的图象.若
的图象.若![]() 图象的一个对称中心为
图象的一个对称中心为![]() ,求
,求![]() 的最小值;
的最小值;
(3)在(2)条件下,求![]() 在
在![]() 上的增区间.
上的增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com