
【题目】2016里约奥运会期间,小赵常看的4个电视频道中有2个频道在转播奥运比赛,若小赵这时打开电视,随机打开其中两个频道试看,那么,小赵所看到的第一个电视台恰好没有转播奥运比赛,而第二个电视台恰好在转播奥运比赛的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】某种产品的质量用其质量指标值来衡量)质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
![]() 配方的频数分布表:
配方的频数分布表:
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110] |
频数 | 8 | 20 | 42 | 22 | 8 |
![]() 配方的频数分布表:
配方的频数分布表:
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106] | [106,110] |
频数 | 4 | 12 | 42 | 32 | 10 |
(1)分别估计用![]() 配方、
配方、![]() 配方生产的产品的优质品率;
配方生产的产品的优质品率;
(2)已知用![]() 配方生产的一件产品的利润(单位:元)与其质量指标值
配方生产的一件产品的利润(单位:元)与其质量指标值![]() 的关系为
的关系为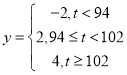 ,估计用
,估计用![]() 配方生产的一件产品的利润大于
配方生产的一件产品的利润大于![]() 的概率,并求用
的概率,并求用![]() 配方生产的上述
配方生产的上述![]() 件产品的平均利润.
件产品的平均利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图(已知本次测试成绩满分100分,且均为不低于50分的整数),请根据图表中的信息解答下列问题.
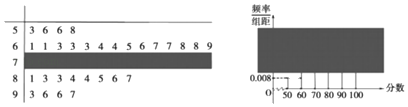
(1)求全班的学生人数及频率分布直方图中分数在[70,80)之间的矩形的高;
(2)为了帮助学生提高数学成绩,决定在班里成立“二帮一”小组,即从成绩[90,100]中选两位同学,共同帮助[50,60)中的某一位同学,已知甲同学的成绩为53分,乙同学的成绩为96分,求甲、乙恰好被安排在同一小组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为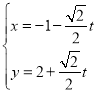 (其中
(其中![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为常数,且
为常数,且![]() ),直线
),直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求实数
,求实数![]() 的值;
的值;
(2)若点![]() 的直角坐标为
的直角坐标为![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形为面的多面体,体现了数学的对称美.如图,将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,如此共可截去八个三棱锥,得到一个有十四个面的半正多面体,它们的棱长都相等,其中八个为正三角形,六个为正方形,称这样的半正多面体为二十四等边体.若棱长为![]() 的二十四等边体的各个顶点都在同一个球面上,则该球的表面积为( )
的二十四等边体的各个顶点都在同一个球面上,则该球的表面积为( )
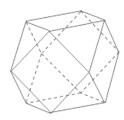
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在梯形ABCD中,![]() ,
,![]() ,
,![]() ,过A,B分别作CD的垂线,垂足分别为E,F,已知
,过A,B分别作CD的垂线,垂足分别为E,F,已知![]() ,
,![]() ,将梯形ABCD沿AE,BF同侧折起,使得平面
,将梯形ABCD沿AE,BF同侧折起,使得平面![]() 平面ABFE,平面
平面ABFE,平面![]() 平面BCF,得到图2.
平面BCF,得到图2.
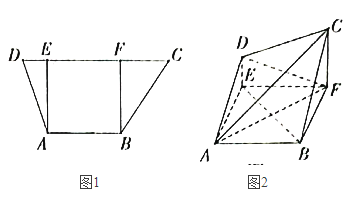
(1)证明:![]() 平面ACD;
平面ACD;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com