
【题目】某校某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图(已知本次测试成绩满分100分,且均为不低于50分的整数),请根据图表中的信息解答下列问题.
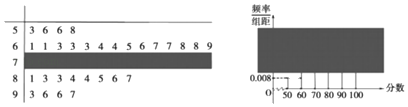
(1)求全班的学生人数及频率分布直方图中分数在[70,80)之间的矩形的高;
(2)为了帮助学生提高数学成绩,决定在班里成立“二帮一”小组,即从成绩[90,100]中选两位同学,共同帮助[50,60)中的某一位同学,已知甲同学的成绩为53分,乙同学的成绩为96分,求甲、乙恰好被安排在同一小组的概率.
【答案】(1)50人,0.04;(2)![]()
【解析】
(1)先根据频数计算在[50,60)上的频率,继而求得全班总人数,再根据[70,80)之间的人数求得[70,80)之间的频率与高即可.
(2)根据题意求得[50,60)中的人数与[90,100)分数段内的人数,再编号利用枚举法求解即可.
(1)由茎叶图知分数在[50,60)上的频数为4,
频率为0.008×10=0.08,
故全班的学生人数为![]() 50人,
50人,
∵分数在[70,80)间的频数为:50﹣(4+14+8+4)=20,
∴频率是![]() ,∴矩形的高是
,∴矩形的高是![]() 0.04.
0.04.
(2)成绩在[50,60)分数段内的人数有4人,记为甲、A、B、C,
成绩在[90,100)分数段内的人数有4人,记为乙、a,b,c,
则“二帮一”小组有以下24种分组办法:
甲乙a,甲乙b,甲乙c,甲ab,甲ac,甲bc,A乙a,A乙b,
A乙c,Aab,Aac,Abc,B乙a,B乙b,B乙c,Bab,
Bac,Bbc,C乙a,C乙b,C乙c,Cab,Cac,Cbc,
其中,甲、乙两同学被分在同一小组有3种办法:甲乙a,甲乙b,甲乙c,
∴甲乙两同学恰好被安排在同一小组的概率为P![]() .
.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】下图是某省从1月21日至2月24日的新冠肺炎每日新增确诊病例变化曲线图.

若该省从1月21日至2月24日的新冠肺炎每日新增确诊人数按日期顺序排列构成数列![]() ,
,![]() 的前n项和为
的前n项和为![]() ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.数列![]() 是递增数列B.数列
是递增数列B.数列![]() 是递增数列
是递增数列
C.数列![]() 的最大项是
的最大项是![]() D.数列
D.数列![]() 的最大项是
的最大项是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为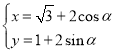 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() ,(t为参数),在以原点为极点,x轴正半轴为极轴的极坐标中,曲线
,(t为参数),在以原点为极点,x轴正半轴为极轴的极坐标中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将![]() 与
与![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)若曲线![]() 与
与![]() 的公共点都在
的公共点都在![]() 上,
上,![]() ,求r.
,求r.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)过点(1,
(a>b>0)过点(1,![]() ),过椭圆C的一个焦点作与长轴垂直的直线,被椭圆C截得的弦长为1
),过椭圆C的一个焦点作与长轴垂直的直线,被椭圆C截得的弦长为1
(1)求椭圆C的标准方程
(2)已知点P为椭圆C上不同于顶点的一点,A,B为椭圆C的左,右顶点,直线AP,BP分别与直线x=﹣6交于M,N两点设线段MN中点为Q,求![]() 的取最小值时点Q的坐标.
的取最小值时点Q的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点A是直线
,点A是直线![]() 上的动点,过
上的动点,过![]() 作直线
作直线![]() ,
,![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 交于点
交于点![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若点![]() ,
,![]() 是直线
是直线![]() 上两个不同的点,且
上两个不同的点,且![]() 的内切圆方程为
的内切圆方程为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016里约奥运会期间,小赵常看的4个电视频道中有2个频道在转播奥运比赛,若小赵这时打开电视,随机打开其中两个频道试看,那么,小赵所看到的第一个电视台恰好没有转播奥运比赛,而第二个电视台恰好在转播奥运比赛的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)分别求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,交曲线
两点,交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com