
【题目】设函数![]() .
.
(1)当![]() 时,若
时,若![]() 在
在![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 在
在![]() ,
,![]() 处取得极值,且方程
处取得极值,且方程![]() 在
在![]() 上有唯一解时,
上有唯一解时,![]() 的取值范围为
的取值范围为![]() 或
或![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1) 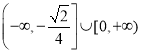 ;(2)
;(2)![]() .
.
【解析】
(1)当![]() 时,函数
时,函数![]() ,其导函数为
,其导函数为![]() 通过若
通过若![]() 在
在![]() 上是单调函数,对
上是单调函数,对![]() 的讨论,即可求得实数
的讨论,即可求得实数![]() 的取值范围;
的取值范围;
(2)先求出导函数 ![]() ,由
,由![]() 在
在![]() 处取得极值,可得
处取得极值,可得![]() .代入解得
.代入解得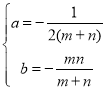 ,此时导函数可化为
,此时导函数可化为![]() 由
由![]() ,可知
,可知![]() 的单调性可判断
的单调性可判断![]() 是
是![]() 在
在![]() 上的极小值,
上的极小值,![]() 是
是![]() 在
在![]() 上的极大值,要使方程
上的极大值,要使方程![]() 在
在![]() 上有唯一解时,
上有唯一解时,![]() 的取值范围为
的取值范围为![]() 或
或![]() 只有可能
只有可能![]() ,即求
,即求![]() 的最大值只需求
的最大值只需求![]() 的最大值即可.由
的最大值即可.由![]() . 令
. 令![]() ,可知
,可知![]() ,则有
,则有![]() 构造
构造![]() ,利用导数研究其最值即可.
,利用导数研究其最值即可.
(1)当![]() 时,函数
时,函数![]() ,其导函数为
,其导函数为![]()
当![]() 时,
时,![]() ,因为
,因为![]() 所以
所以![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() ,则
,则![]() 在
在![]() 上单调递增.
上单调递增.
当![]() 时,设
时,设![]() ,其对称轴为
,其对称轴为![]() ,若
,若![]() 在
在![]() 上是单调函数,只能使
上是单调函数,只能使![]() 恒成立,则需满足
恒成立,则需满足![]() 解得
解得![]() ,此时
,此时![]() 在
在![]() 上单调递减.
上单调递减.
综上得![]() 的取值范围是
的取值范围是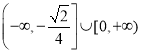
(2) ![]() .
.
![]() 在
在![]() 处取得极值,
处取得极值,![]() .
.
即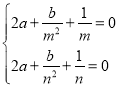 ,解得
,解得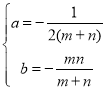
所以可得![]() 令
令![]() ,解得
,解得![]() ,令
,令![]() ,解得
,解得![]() 或
或![]() .
.
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
所以![]() 是
是![]() 在
在![]() 上的极小值,
上的极小值,![]() 是
是![]() 在
在![]() 上的极大值.
上的极大值.
若使方程![]() 只有唯一解的
只有唯一解的![]() 的取值范围为
的取值范围为![]() 或
或![]() ,结合函数单调性可得只有可能
,结合函数单调性可得只有可能![]() ,所以求
,所以求![]() 的最大值只需求
的最大值只需求![]() 的最大值即可.
的最大值即可.
又![]() .
.
所以![]() .
.
记![]() 则
则![]() ,则
,则![]() .
.
令![]() ,其导函数为
,其导函数为![]()
当![]() 时,
时,![]() ,故
,故![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,故
,故![]() 单调递减.
单调递减.
所以![]() 的最大值为
的最大值为![]() .所以
.所以![]() 的最大值为
的最大值为![]() .
.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,
,![]() 为
为![]() 上任意一点,
上任意一点,![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,记点
,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知点![]() ,过
,过![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点,证明:直线
两点,证明:直线![]() 的斜率与直线
的斜率与直线![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其中左焦点
,其中左焦点![]() (-2,0).
(-2,0).
(1) 求椭圆C的方程;
(2) 若直线y=x+m与椭圆C交于不同的两点A,B,且线段AB的中点M在圆x2+y2=1上,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图(已知本次测试成绩满分100分,且均为不低于50分的整数),请根据图表中的信息解答下列问题.
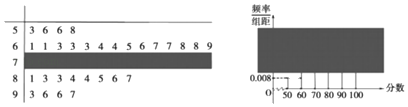
(1)求全班的学生人数及频率分布直方图中分数在[70,80)之间的矩形的高;
(2)为了帮助学生提高数学成绩,决定在班里成立“二帮一”小组,即从成绩[90,100]中选两位同学,共同帮助[50,60)中的某一位同学,已知甲同学的成绩为53分,乙同学的成绩为96分,求甲、乙恰好被安排在同一小组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
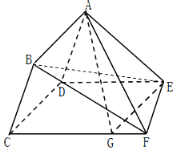
【题目】如图,在多面体ABCDEF中,四边形ABCD为平行四边形,平面ADE⊥平面CDEF,∠ADE=60°,DE∥CF,CD⊥DE,AD=2,DE=DC=3,CF=4,点G是棱CF上的动点.
(Ⅰ)当CG=3时,求证EG∥平面ABF;
(Ⅱ)求直线BE与平面ABCD所成角的正弦值;
(Ⅲ)若二面角G﹣AE﹣D所成角的余弦值为![]() ,求线段CG的长.
,求线段CG的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为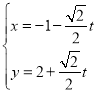 (其中
(其中![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为常数,且
为常数,且![]() ),直线
),直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求实数
,求实数![]() 的值;
的值;
(2)若点![]() 的直角坐标为
的直角坐标为![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,已知ban-2n=(b-1)Sn.
(1)证明:当b=2时,{an-n·2n-1}是等比数列;
(2)求{an}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com