
【题目】如图,多面体![]() 中,四边形
中,四边形![]() 是
是![]() 为钝角的平行四边形,四边形
为钝角的平行四边形,四边形![]() 为直角梯形,
为直角梯形,![]() 且
且![]() .
.
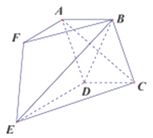
(1)求证:![]() ;
;
(2)若点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)利用勾股定理证得![]() ,结合
,结合![]() ,证得
,证得![]() 平面
平面![]() ,根据线线平行证得
,根据线线平行证得![]() 平面
平面![]() ,由此证得
,由此证得![]() .判断出四边形
.判断出四边形![]() 为菱形,由此证得
为菱形,由此证得![]() ,由此证得
,由此证得![]() 平面
平面![]() ,从而证得
,从而证得![]() .
.
(2)利用第一问的结论,判断出线![]() 与平面
与平面![]() 所成角,结合点
所成角,结合点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,求得
,求得![]() 的长,然后通过解三角形,把相应的线面角的正弦值求出.
的长,然后通过解三角形,把相应的线面角的正弦值求出.
(1)在![]() 中,
中,![]() ,所以
,所以![]()
又因为![]() ,所以
,所以![]() 平面
平面![]() ,因为
,因为![]()
所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
在平行四边形![]() 中,且
中,且![]() ,所以平行四边形
,所以平行四边形![]() 为菱形
为菱形
于是![]()
所以![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() .
.
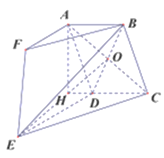
(2)因为![]() 平面
平面![]() 且垂足为
且垂足为![]() ,所以
,所以![]() 为直线
为直线![]() 与平面
与平面![]() 所成角.
所成角.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所
,所![]() ,
,
所以![]() 到平面
到平面![]() 的距离为
的距离为![]() 到平面
到平面![]() 的距离.
的距离.![]()
所以![]() 平面
平面![]() 平面
平面![]()
所以平面![]() 平面
平面![]() 且交线为
且交线为![]()
过![]() 作
作![]() ,则
,则![]() ,所以
,所以![]()
所以![]() ,所以
,所以![]()
在![]() 中,
中,![]() ,
,
所以![]() .所以直线
.所以直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为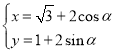 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() ,(t为参数),在以原点为极点,x轴正半轴为极轴的极坐标中,曲线
,(t为参数),在以原点为极点,x轴正半轴为极轴的极坐标中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将![]() 与
与![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)若曲线![]() 与
与![]() 的公共点都在
的公共点都在![]() 上,
上,![]() ,求r.
,求r.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016里约奥运会期间,小赵常看的4个电视频道中有2个频道在转播奥运比赛,若小赵这时打开电视,随机打开其中两个频道试看,那么,小赵所看到的第一个电视台恰好没有转播奥运比赛,而第二个电视台恰好在转播奥运比赛的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(k+![]() )lnx+
)lnx+![]() ,k∈[4,+∞),曲线y=f(x)上总存在两点M(x1,y1),N(x2,y2),使曲线y=f(x)在M,N两点处的切线互相平行,则x1+x2的取值范围为
,k∈[4,+∞),曲线y=f(x)上总存在两点M(x1,y1),N(x2,y2),使曲线y=f(x)在M,N两点处的切线互相平行,则x1+x2的取值范围为
A. (![]() ,+∞) B. (
,+∞) B. (![]() ,+∞) C. [
,+∞) C. [![]() ,+∞) D. [
,+∞) D. [![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)分别求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,交曲线
两点,交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com