
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
| s |
| t |
|
| 3 |
| 3 |
| s |
| t |
| 3 |
| 6 |
| 6 |
| 6 |
|
| 3 |
| y2 |
| 3 |
| s |
| t |
| 3 |
2
| ||||
|
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| k |
| 3 |
|3k-
| ||
|
|
| ||
|
3-(
|
|
1-(
|
|
| S |
| t |
|
|
| 3 |
| s |
| t |
| 3 |


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| ���乤�� | ;���ٶ� ��ǧ��/ʱ�� |
��;�з��� ��Ԫ/ǧ�ף� |
װж���ã�Ԫ�� | ��װжʱ�� ��Сʱ�� |
����װж��ķ��ã�Ԫ/Сʱ�� |
| ���ɻ� | ��200 | ��15 | ��1000 | ��2 | 200 |
| ���� | ��100 | ��4 | ��2000 | ��4 | 200 |
| ������ | ��50 | ��8 | ��700 | ��3 | 200 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
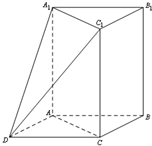 ��ͼ��������ABC-A1B1C1�У�AA1��ƽ��ABC����ACB=90�㣬AC=BC=1��AA1=2����AB��BCΪ�ڱ���ƽ���ı���ABCD������DA1��DC1��
��ͼ��������ABC-A1B1C1�У�AA1��ƽ��ABC����ACB=90�㣬AC=BC=1��AA1=2����AB��BCΪ�ڱ���ƽ���ı���ABCD������DA1��DC1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
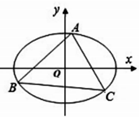 ��֪��ԲC��
��֪��ԲC��| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
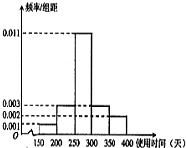 ��ij���ܵ��������������ȡ100����Ʒ�����������飬������ʹ��ʱ�䣨��λ���죩����5�飬�õ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��
��ij���ܵ��������������ȡ100����Ʒ�����������飬������ʹ��ʱ�䣨��λ���죩����5�飬�õ�Ƶ�ʷֲ�ֱ��ͼ��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
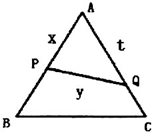 ��֪��ABC�DZ߳�Ϊ2���������Σ�P��Q������AB��AC���ϵĵ㣬���߶�PQ����ABC�ֳ������ȵ������֣���AP=x��AQ=t��PQ=y����
��֪��ABC�DZ߳�Ϊ2���������Σ�P��Q������AB��AC���ϵĵ㣬���߶�PQ����ABC�ֳ������ȵ������֣���AP=x��AQ=t��PQ=y�����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com