
| 3 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:
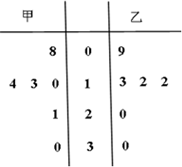 在如图所示的茎叶图中,甲、乙两组数据的平均数分别为
在如图所示的茎叶图中,甲、乙两组数据的平均数分别为. |
| x甲 |
. |
| x乙 |
. |
| S甲 |
. |
| S乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| m |
| n |
| m |
| n |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 3 |
| b |
| a |
| b |
| π |
| 6 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2-6x+9 |
| x2+8x+16 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 达州市万源中学实施“阳光体育”素质教育,要求学生在校期间每天上午第二节课下课后迅速到操场参加课间活动.现调查高三某班学生从教室到操场路上所需时间(单位:分钟)并将所得数据绘制成频率直方图(如图),其中,路上所需时间的范围是(0,10],样本数据分组为(0,2),[2,4),[4,6),[6,8),[8,10].
达州市万源中学实施“阳光体育”素质教育,要求学生在校期间每天上午第二节课下课后迅速到操场参加课间活动.现调查高三某班学生从教室到操场路上所需时间(单位:分钟)并将所得数据绘制成频率直方图(如图),其中,路上所需时间的范围是(0,10],样本数据分组为(0,2),[2,4),[4,6),[6,8),[8,10].查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| 1 |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com