
(根据2013年高考冲刺卷改编)函数 ,
, ,其中
,其中
(1)当m=n+6时,函数f(x)有两个极值点 .
.
 求n的取值范围;
求n的取值范围;
 求
求 .
.
(2) ,若函数f(x),g(x)在区间
,若函数f(x),g(x)在区间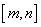 上分别为单调递增和递减函数,求n-m的最大值.
上分别为单调递增和递减函数,求n-m的最大值.
科目:高中数学 来源: 题型:
如图,四棱锥 中,平面
中,平面
 平面
平面 ,
,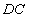 //
//  ,
, ,
,
 ,且
,且 ,
, .
.
(I)求证: 平面
平面 ;
;
(II)求 和平面
和平面 所成角的正弦值;
所成角的正弦值;
 (III)在线段
(III)在线段 上是否存在一点
上是否存在一点 使得平面
使得平面
 平面
平面 ,请说明理由.
,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
设A1,A2,A3,A4是平面直角坐标系中两两不同的四点,若=λ(λ∈R),=μ(μ∈R),且+=2,则称A3,A4调和分割A1,A2,已知平面上的点C,D调和分割点A,B,则下面说法正确的是 ( )
A.C可能是线段AB的中点
B.D可能是线段AB的中点
C.C,D可能同时在线段AB上
D.C,D不可能同时在线段AB的延长线上
查看答案和解析>>
科目:高中数学 来源: 题型:
设 是空间中的一个平面,
是空间中的一个平面, 是三条不同的直线,则 ( )
是三条不同的直线,则 ( )
①若 ; ②若
; ②若
③若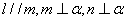 ,则
,则 ④若
④若 ;
;
则上述命题中正确的是 ( )
A.①② B.②③ C.③④ D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com