
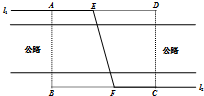
 如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线l1排,在路南侧沿直线l2排,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成的小于90°的角为α.
如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线l1排,在路南侧沿直线l2排,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成的小于90°的角为α.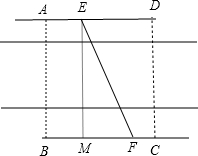
| 4 |
| 3 |
| 60 |
| cosα |
| 60 |
| cosα |
| 60sinα |
| cosα |
| 120 |
| cosα |
| 60(sinα-2) |
| cosα |
| sinα-2 |
| cosα |
| 4 |
| 3 |
| cosα•cosα-(-sinα)•(sinα-2) |
| cos2α |
| 1-2sinα |
| cos2α |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 3 |
| 3 |
| 3 |
| π |
| 6 |


科目:高中数学 来源: 题型:
 如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线排l1,在路南侧沿直线排l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=60
如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线排l1,在路南侧沿直线排l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=60| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
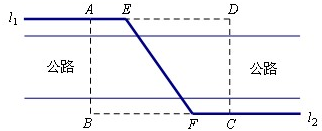
科目:高中数学 来源:2013-2014学年江苏南京金陵中学高三第一学期期中考试理科数学试卷(解析版) 题型:解答题
如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB = 60m,BC = 80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB= α,矩形区域内的铺设水管的总费用为W.

(1)求W关于α的函数关系式;
(2)求W的最小值及相应的角α.
查看答案和解析>>
科目:高中数学 来源:2014届江苏省苏州市高三暑假自主学习测试理科数学试卷(解析版) 题型:解答题
如图,某自来水公司要在公路两侧排水管,公路为东西方向,在路北侧沿直线 排,在路南侧沿直线
排,在路南侧沿直线 排,现要在矩形区域
排,现要在矩形区域 内沿直线将
内沿直线将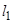 与
与 接通.已知
接通.已知 ,
, ,公路两侧排管费用为每米1万元,穿过公路的
,公路两侧排管费用为每米1万元,穿过公路的 部分的排管费用为每米2万元,设
部分的排管费用为每米2万元,设 与
与 所成的小于
所成的小于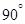 的角为
的角为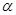 .
.

(Ⅰ)求矩形区域 内的排管费用
内的排管费用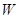 关于
关于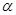 的函数关系式;
的函数关系式;
(Ⅱ)求排管的最小费用及相应的角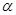 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com