【答案】
分析:解法一:
在含有直线与平面垂直垂直的条件的棱柱、棱锥、棱台中,可以建立空间直角坐标系,设定参量求解.比如此题中,我们可以以A为坐标原点,分别以AB、AD、AA
1为x、y、z轴,建立空间直角坐标系O-xyz.这种解法的好处就是:①解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理,因为这些可以用向量方法来解决.②即使立体感稍差一些的学生也可以顺利解出,因为只需画个草图以建立坐标系和观察有关点的位置即可.
(I)∵
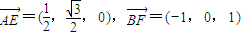
,∴
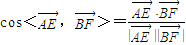
.即异面直线AE、BF所成的角为
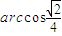
.
(II)易知平面AA
1B的一个法向量
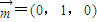
.设
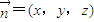
是平面BDF的一个法向量,即平面BDF与平面AA
1B所成二面角(锐角)大小为向量.
(III)点A到平面BDF的距离,即
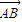
在平面BDF的法向量
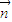
上的投影的绝对值,所以距离
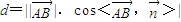
解法二:
(I)求异面直线所成的角,也可以做适当的平移,把异面直线转化为相交直线,然后在相关的三角形中借助正弦或余弦定理解出所求的角.平移时主要是根据中位线和中点条件,或者是特殊的四边形,三角形等.连接B
1D
1,过F作B
1D
1的垂线,垂足为K,则FK∥AE.∴∠BFK为异面直线BF与AE所成的角.
(II)二面角的度量关键在于找出它的平面角,构造平面角常用的方法就是三垂线法.由于DA⊥面AA
2B,由A作BF的垂线AG,垂足为G,连接DG,由三垂线定理知BG⊥DG.∴∠AGD即为平面BDF与平面AA
1B所成二面角的平面角.
(III)在立体几何中,求点到平面的距离是一个常见的题型,同时求直线到平面的距离、平行平面间的距离及多面体的体积也常转化为求点到平面的距离.找(作)出一个过该点的平面与已知平面垂直,然后过该点作其交线的垂线,则得点到平面的垂线段.由(II)知平面AFD是平面BDF与平面AA
1B所成二面确的平面角所在的平面∴面AFD⊥面BDF.在Rt△ADF,由A作AH⊥DF于H,则AH即为点A到平面BDF的距离.
解答: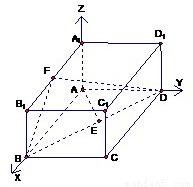
解:法一:在长方体ABCD-A
1B
1C
1D
1中,以AB所在直线为x轴,AD所在直线为y
轴,AA
1所在直线为z轴建立空间直角坐标系如图.
由已知AB=2,AA
1=1,可得A(0,0,0),B(2,0,0),F(1,0,1).
又AD⊥平面AA
1B
1B,从而BD与平面AA
1B
1B所成的角即为∠DBA=30°,
又
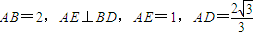
,
从而易得
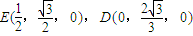
.
(I)∵
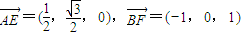
,
∴
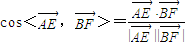
=
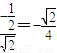
.
即异面直线AE、B所成的角为
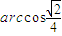
.]
(II)易知平面AA
1B的一个法向量
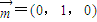
.
设
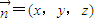
是平面BDF的一个法向量,
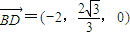
.
由
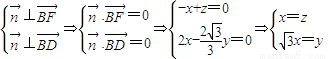
,
取
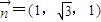
,∴
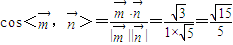
.
即平面BDF与平面AA
1B所成二面角(锐角)大小为
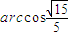
.
(III)点A到平面BDF的距离,即
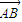
在平面BDF的法向量
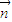
上的投影的绝对值,
所以距离
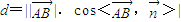
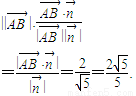
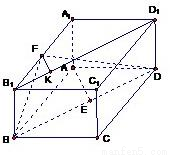
所以点A到平面BDF的距离为
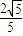
.
解法二:(I)连接B
1D
1,过F作B
1D
1的垂线,
垂足为K,∵BB
1与两底面ABCD,A
1B
1C
1D
1都垂直,
∴
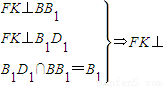
平面BDD
1B
1,
又
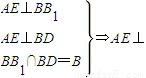
平面BDD
1B
1,
因此FK∥AE.∴∠BFK为异面直线BF与AE所成的角.
连接BK,由FK⊥面BDD
1B
1得FK⊥BK,
从而△BKF为Rt△.
在Rt△B
1KF和Rt△B
1D
1A
1中,
由
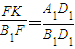
得
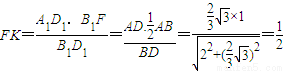
.
又
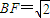
,∴
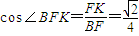
.
∴异面直线BF与AE所成的角为
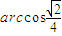
.
(II)由于DA⊥面AA
2B,由A作BF的垂线AG,垂足为G,
连接DG,由三垂线定理知BG⊥DG.
∴∠AGD即为平面BDF与平面AA
1B所成二面角的平面角,
且∠DAG=90°,在平面AA
1B中,延长BF与AA
1交于
点S,∵F为A
2B
1的中点,A
1F∥=
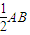
,
即SA=2A
1A=2=AB,∴Rt△BAS为等腰直角三角形,
垂足G点为斜边SB的中点F,即F、G重合.
易得
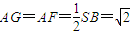
.在Rt△BAS中,
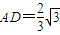
.
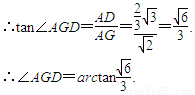
即平面BDF与平面AA
1B所成二面角(锐角)的大小为
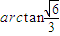
.
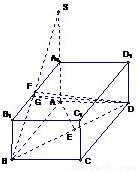
(III)由(II)知平面AFD是平面BDF与平面AA
1B所
成二面确的平面角所在的平面∴面AFD⊥面BDF.
在Rt△ADF,由A作AH⊥DF于H,则AH即为点
A到平面BDF的距离.
由AH.DF=AD.AF,
得
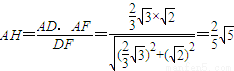
.
所以点A到平面BDF的距离为
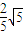
.
点评:本小题主要考查空间线面关系、面面关系、二面角的度量、点到面的距离计算,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

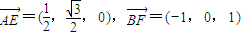 ,∴
,∴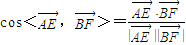 .即异面直线AE、BF所成的角为
.即异面直线AE、BF所成的角为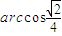 .
.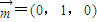 .设
.设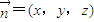 是平面BDF的一个法向量,即平面BDF与平面AA1B所成二面角(锐角)大小为向量.
是平面BDF的一个法向量,即平面BDF与平面AA1B所成二面角(锐角)大小为向量.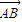 在平面BDF的法向量
在平面BDF的法向量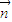 上的投影的绝对值,所以距离
上的投影的绝对值,所以距离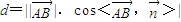
 解:法一:在长方体ABCD-A1B1C1D1中,以AB所在直线为x轴,AD所在直线为y
解:法一:在长方体ABCD-A1B1C1D1中,以AB所在直线为x轴,AD所在直线为y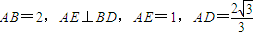 ,
,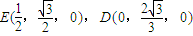 .
.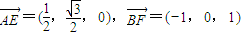 ,
,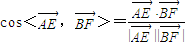 =
=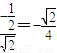 .
.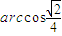 .]
.]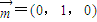 .
.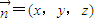 是平面BDF的一个法向量,
是平面BDF的一个法向量,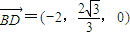 .
.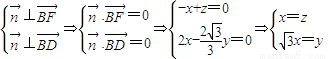 ,
,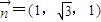 ,∴
,∴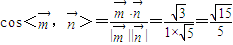 .
.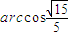 .
.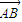 在平面BDF的法向量
在平面BDF的法向量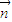 上的投影的绝对值,
上的投影的绝对值,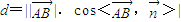
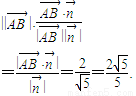

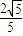 .
.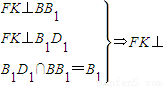 平面BDD1B1,
平面BDD1B1,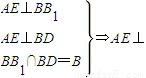 平面BDD1B1,
平面BDD1B1,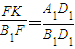
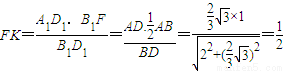 .
.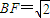 ,∴
,∴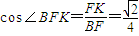 .
.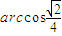 .
.
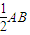 ,
,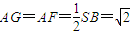 .在Rt△BAS中,
.在Rt△BAS中,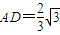 .
.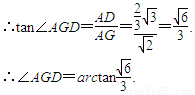
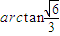 .
.
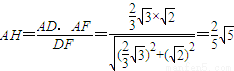 .
. .
.

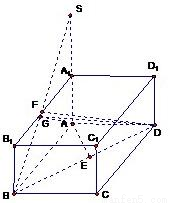
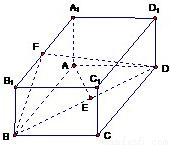
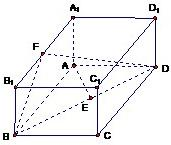 如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于E,F为A1B1的中点.
如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于E,F为A1B1的中点. 如图,已知长方体ABCD-A1B1C1D1中,AB=2
如图,已知长方体ABCD-A1B1C1D1中,AB=2 如图,已知长方体ABCD-A1B1C1D1中,AB=3,AD=AA1=2,点O是线段BC1的中点,点M是OD的中点,点E是线段AB上一点,AE>BE,且A1E⊥OE.
如图,已知长方体ABCD-A1B1C1D1中,AB=3,AD=AA1=2,点O是线段BC1的中点,点M是OD的中点,点E是线段AB上一点,AE>BE,且A1E⊥OE. 如图,已知长方体ABCD-A′B′C′D′中,AB=2
如图,已知长方体ABCD-A′B′C′D′中,AB=2 (2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F
(2008•宣武区一模)如图,已知长方体AC1中,AB=BC=1,BB1=2,连接B1C,过B点作B1C的垂线交CC1于E,交B1C于F