
 和所支出的维修费用
和所支出的维修费用 (万元)的几组对照数据:
(万元)的几组对照数据: (年) (年) |  |  |  |  |
 (万元) (万元) |  |  |  |  |
 对
对 呈线性相关关系,请根据上表提供的数据,用最小二乘法求出
呈线性相关关系,请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
 ;预测该型号设备技改后使用10年的维修费用比技改前降低1.65万元。
;预测该型号设备技改后使用10年的维修费用比技改前降低1.65万元。
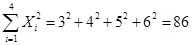


 ;
; 

 =10时,
=10时,  ,
,  (万元)
(万元)  ;预测该型号设备技改后使用10年的维修费用比技改前降低1.65万元。
;预测该型号设备技改后使用10年的维修费用比技改前降低1.65万元。

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:单选题
 ,叙述正确的是
,叙述正确的是A. 越大,相关程度越大,反之相关程度越小 越大,相关程度越大,反之相关程度越小 |
B. 越大,相关程度越大,反之相关程度越小 越大,相关程度越大,反之相关程度越小 |
C.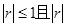 越接近1,相关程度越大 越接近1,相关程度越大 |
| D.以上说法都不对 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 必过
必过 ;
; 的零点有2个;
的零点有2个; 的图象与
的图象与 轴围成的图形面积是
轴围成的图形面积是 ;
; 是偶函数,且在区间
是偶函数,且在区间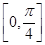 内单调递增;
内单调递增; 的最小正周期为
的最小正周期为 .其中真命题的序号是 。
.其中真命题的序号是 。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.一组数据的平均数一定大于这组数据中的每个数据 |
| B.一组数据不可能有两个众数 |
| C.一组数据的中位数一定是这组数据中的某个数据 |
| D.一组数据的方差越大,说明这组数据的波动越大 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.相关关系的两个变量不是因果关系 |
| B.散点图能直观地反映数据的相关程度 |
| C.回归直线最能代表线性相关的两个变量之间的关系 |
| D.任一组数据都有回归方程 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 之间的一组数据如下:
之间的一组数据如下: | 0 | 1 | 2 | 3 | 4 |
 | 2.2 | 4.3 | 4.5 | 4.8 | 6.7 |
 ,其中
,其中 .则当
.则当 时,
时, 的预测值为( )
的预测值为( )查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
 =bx+a,其中b=-20,a=
=bx+a,其中b=-20,a= -b
-b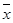 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 月份x | 1 | 2 | 3 | 4 |
| 用水量y(100t) | 4.4 | 4 | 3 | 2.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com