
一个袋中装有四个形状大小完全相同的球,球的编号分别为 ,
,
(1)从袋中随机取出两个球,求取出的球的编号之和不大于 的概率;
的概率;
(2)先从袋中随机取一个球,该球的编号为 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为 ,求
,求 的概率.
的概率.
(1)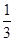 ;(2)
;(2)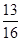
解析试题分析:(1)从袋子中随机取两个球,其一切可能的结果组成的基本事件有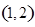 ,
,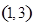 ,
,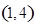 ,
,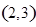 ,
,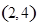 ,
,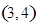 共6个。从袋中随机取出的球的编号之和不大于4的事件共有
共6个。从袋中随机取出的球的编号之和不大于4的事件共有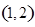 ,
,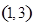 两个。因此所求事件的概率为
两个。因此所求事件的概率为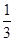 。 6分
。 6分
(2)先从袋中随机取一个球,记下编号为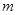 ,放回后,在从袋中随机取一个球,记下编号为
,放回后,在从袋中随机取一个球,记下编号为 ,其一切可能的结果
,其一切可能的结果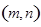 有:
有: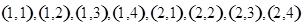 ,
,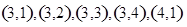
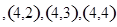 共16个有满足条件
共16个有满足条件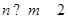 的事件为
的事件为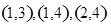 共3个所以满足条件
共3个所以满足条件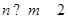 的事件的概率为
的事件的概率为 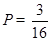
故满足条件n<m+2 的事件的概率为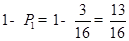 12分
12分
考点:本题考查了古典概型的求法
点评:对于古典概型的概率的计算,首先要分清基本事件总数及事件A包含的基本事件数,分清的方法常用列表法、画图法、列举法、列式计算等方法,还要注意结合求概率的其它公式求古典概型的概率


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(1)甲盒中有红,黑,白三种颜色的球各3个,乙盒子中有黄,黑,白三种颜色的球各2个,从两个盒子中各取1个球,求取出的两个球是不同颜色的概率。
(2)在单位圆的圆周上随机取三点A、B、C,求 是锐角三角形的概率。
是锐角三角形的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分) 某工厂组织工人参加上岗测试,每位测试者最多有三次机会,一旦某次测试通过,便可上岗工作,不再参加以后的测试;否则就一直测试到第三次为止。设每位工人每次测试通过的概率依次为0.2,0.5,0.5,每次测试相互独立。
(1)求工人甲在这次上岗测试中参加考试次数为2、3的概率分别是多少?
(2)若有4位工人参加这次测试,求至少有一人不能上岗的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设关于 的一元二次方程
的一元二次方程 .
.
(1)若 ,
, 都是从集合
都是从集合 中任取的数字,求方程有实根的概率;
中任取的数字,求方程有实根的概率;
(2)若 是从区间[0,4]中任取的数字,
是从区间[0,4]中任取的数字, 是从区间[1,4]中任取的数字,求方程有实根的概率.
是从区间[1,4]中任取的数字,求方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取3次,每次摸取一个球。
(1)试问:一共有多少种不同的结果?请列出所有可能的结果;
(2)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某项计算机考试按科目A、科目B依次进行,只有大拿感科目A成绩合格时,才可继续参加科目B的考试,已知每个科目只允许有一次补考机会,两个科目均合格方快获得证书,现某人参加这项考试,科目A每次考试成绩合格的概率为 ,科目B每次考试合格的概率为
,科目B每次考试合格的概率为 ,假设各次考试合格与否均互不影响.
,假设各次考试合格与否均互不影响.
(Ⅰ)求他不需要补考就可获得证书的概率;
(Ⅱ)在这次考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为 ,求随即变量
,求随即变量 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在平面直角坐标系 中,平面区域
中,平面区域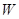 中的点的坐标
中的点的坐标 满足
满足 ,从区域
,从区域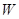 中随机取点
中随机取点 .
.
(Ⅰ)若 ,
, ,求点
,求点 位于第四象限的概率;
位于第四象限的概率;
(Ⅱ)已知直线 与圆
与圆 相交所截得的弦长为
相交所截得的弦长为 ,求
,求 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)将52名志愿者分成A,B两组参加义务植树活动,A组种植150捆白杨树苗,B组种植200捆沙棘树苗. 假定A,B两组同时开始植树.
(1)根据历年统计,每名志愿者种植一捆白杨树苗用时 小时,种植一捆沙棘用时
小时,种植一捆沙棘用时 小时,应如何分配A,B两组的人数,使植树活动持续的时间最短?
小时,应如何分配A,B两组的人数,使植树活动持续的时间最短?
(2)在按(1)分配的人数种植1小时后发现,每名志愿者种植一捆白杨仍用时 小时,而每名志愿者种植一捆沙棘实际用时
小时,而每名志愿者种植一捆沙棘实际用时 小时,于是,从A组抽调6名志愿者加入B组继续种植,求植树活动持续的时间.
小时,于是,从A组抽调6名志愿者加入B组继续种植,求植树活动持续的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
.已知关于x的一元二次方程x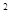 -2(a-2)x-b
-2(a-2)x-b +16=0.
+16=0.
(1)若a、b是一枚骰子先后投掷两次所得到的点数,求方程有两个正实数根的概率;
(2)若a∈[2,6],b∈[0,4],求一元二次方程没有实数根的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com