
上海某化学试剂厂以x 千克/小时的速度生产某种产品(生产条件要求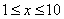 ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是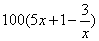 元.
元.
(1)要使生产运输该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产运输900千克该产品获得的利润最大,问:该工厂应该选取何种生产速度?并求最大利润.
 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
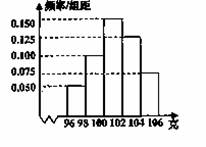
【题文】某工厂对一批产品进行抽样检测,根据抽样检测后的产品净重(单位:g)数据绘制的频率分布直方图如图所示,已知产品净重的范围是区间[96,106],样本中净重在区间[96,100)的产品个数是24,则样本中净重在区间[98,104)的产品个数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com