
【题目】武汉市政府为了给“世界军运会”营造良好交通环境,特招聘了一批交通协管员,这些协管员的年龄都在![]() 之间,按年龄情况对他们进行统计得到的频率分布直方图如下,其中年龄在
之间,按年龄情况对他们进行统计得到的频率分布直方图如下,其中年龄在![]() 岁的有10人,
岁的有10人,![]() 岁的有45人.
岁的有45人.
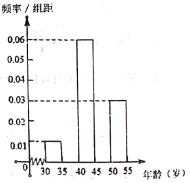
(1)补全频率分布直方图,并估计协管员的年龄中位数;
(2)为感谢年长的协管员的支持,利用分层抽样的方法从年龄在![]() 的协管员中抽取5人,并从这5人中再抽取3人,各赠送一份礼品,求仅有一人年龄在
的协管员中抽取5人,并从这5人中再抽取3人,各赠送一份礼品,求仅有一人年龄在![]() 的概率.
的概率.
【答案】(1)见解析,![]() .(2)
.(2)![]()
【解析】
(1)由![]() 的人数和频率,求出总人数,求出
的人数和频率,求出总人数,求出![]() 的频率,利用频率和为1,求出
的频率,利用频率和为1,求出
![]() 的频率,即可补全直方图,根据直方图,先确定中位数在哪一组,以及占该组的比例,即可求出中位数;
的频率,即可补全直方图,根据直方图,先确定中位数在哪一组,以及占该组的比例,即可求出中位数;
(2)分层抽样从年龄在![]() 的协管员中抽取5人,
的协管员中抽取5人,![]() 中抽3人,
中抽3人,![]() 抽2人,按两组分别进行编号,列出5人中抽取3人的所有情况,统计仅有一人年龄在
抽2人,按两组分别进行编号,列出5人中抽取3人的所有情况,统计仅有一人年龄在![]() 的抽取个数,即可求解.
的抽取个数,即可求解.
解:(1)由![]() 的人数知总人数
的人数知总人数![]() ,
,
所以![]() 的频率为
的频率为![]() ,频率/组距为
,频率/组距为![]() ;
;
![]() 的频率为
的频率为![]() ,
,
所以频率/组距为![]() .
.
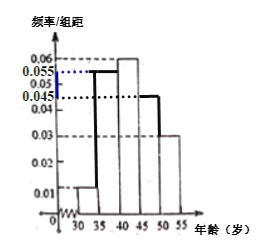
频率分布直方图如图所示:
![]() 所占面积为
所占面积为![]() ,
,![]() 所占面积为
所占面积为![]() ,
,
所以中位数![]() ,且有
,且有![]() ,解得
,解得![]() 为
为![]() .
.
(2)因为![]() ,
,![]() 的人数分别为45人、30人,
的人数分别为45人、30人,
所以分层抽样![]() 中抽3人,记为
中抽3人,记为![]() ,
,
![]() 抽2人,记为
抽2人,记为![]() ,若在这5人中再抽3人,
,若在这5人中再抽3人,
有以下情况:![]() ,
,
![]() ,共有10种抽法,
,共有10种抽法,
仅有一人年龄在![]() 抽法有6种抽法,
抽法有6种抽法,
所以仅有一人年龄在![]() 的概率为
的概率为![]() .
.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】已知动圆![]() 与
与![]() 轴相切,且与圆
轴相切,且与圆![]() :
:![]() 外切;
外切;
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若直线![]() 过定点
过定点![]() ,且与轨迹
,且与轨迹![]() 交于
交于![]() 、
、![]() 两点,与圆
两点,与圆![]() 交于
交于![]() 、
、![]() 两点,若点
两点,若点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求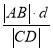 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一项针对某一线城市30~50岁都市中年人的消费水平进行调查,现抽查500名(200名女性,300名男性)此城市中年人,最近一年内购买六类高价商品(电子产品、服装、手表、运动与户外用品、珠宝首饰、箱包)的金额(万元)的频数分布表如下:
女性 | 金额 |
|
|
|
|
|
频数 | 20 | 40 | 80 | 50 | 10 | |
男性 | 金额 |
|
|
|
|
|
频数 | 45 | 75 | 90 | 60 | 30 |
(1)将频率视为概率,估计该城市中年人购买六类高价商品的金额不低于5000元的概率.
(2)把购买六类高价商品的金额不低于5000元的中年人称为“高收入人群”,根据已知条件完成![]() 列联表,并据此判断能否有95%的把握认为“高收入人群”与性别有关?
列联表,并据此判断能否有95%的把握认为“高收入人群”与性别有关?
高收入人群 | 非高收入人群 | 合计 | |
女性 | 60 | ||
男性 | 180 | ||
合计 | 500 |
参考公式: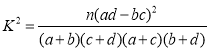 ,其中
,其中![]()
参考附表:
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
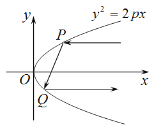
【题目】抛物线有如下光学性质:由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出.现有抛物线![]() ,如图一平行于
,如图一平行于![]() 轴的光线射向抛物线,经两次反射后沿平行
轴的光线射向抛物线,经两次反射后沿平行![]() 轴方向射出,若两平行光线间的最小距离为4,则该抛物线的方程为__________.
轴方向射出,若两平行光线间的最小距离为4,则该抛物线的方程为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 在第一象限内的点
在第一象限内的点![]() 到焦点
到焦点![]() 的距离为
的距离为![]() .
.
(1)若![]() ,过点
,过点![]() ,
, ![]() 的直线
的直线![]() 与抛物线相交于另一点
与抛物线相交于另一点![]() ,求
,求![]() 的值;
的值;
(2)若直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,与圆
两点,与圆![]() 相交于
相交于![]() 两点,
两点, ![]() 为坐标原点,
为坐标原点, ![]() ,试问:是否存在实数
,试问:是否存在实数![]() ,使得
,使得![]() 的长为定值?若存在,求出
的长为定值?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点![]() 、
、![]() 、
、![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() ,
,![]() ,
,![]() 的中点,则下列命题中的真命题是__________(写出所有真命题的序号).
的中点,则下列命题中的真命题是__________(写出所有真命题的序号).
①以正方体的顶点为顶点的三棱锥的四个面中最多可以四个面都是直角三角形;
②点![]() 在直线
在直线![]() 上运动时,总有
上运动时,总有![]() ;
;
③点![]() 在直线
在直线![]() 上运动时,三棱锥
上运动时,三棱锥![]() 的体积是定值;
的体积是定值;
④若![]() 是正方体的面
是正方体的面![]() ,(含边界)内一动点,且点
,(含边界)内一动点,且点![]() 到点
到点![]() 和
和![]() 的距离相等,则点
的距离相等,则点![]() 的轨迹是一条线段.
的轨迹是一条线段.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com