
【题目】记![]() 设
设![]() ,则( )
,则( )
A. 存在![]()
B. 存在![]()
C. 存在![]()
D. 存在![]()
【答案】C
【解析】
求出f(x)的解析式,对t的范围进行讨论,依次判断各选项左右两侧函数的单调性和值域,从而得出答案.
解:x2﹣x3=x2(1﹣x),
∴当x≤1时,x2﹣x3≥0,当x>1时,x2﹣x3<0,
∴f(x)![]() .
.
若t>1,则|f(t)+f(﹣t)|=|t2+(﹣t)3|=|t2﹣t3|=t3﹣t2,
|f(t)﹣f(﹣t)|=|t2+t3|=t2+t3,
f(t)﹣f(﹣t)=t2﹣(﹣t)3=t2+t3,
若0<t<1,|f(t)+f(﹣t)|=|t3+(﹣t)3|=0,
|f(t)﹣f(﹣t)|=|t3+t3|=2t3,
f(t)﹣f(﹣t)=t3﹣(﹣t)3=2t3,
当t=1时,|f(t)+f(﹣t)|=|1+(﹣1)|=0,
|f(t)﹣f(﹣t)|=|1﹣(﹣1)|=2,
f(t)﹣f(﹣t)=1﹣(﹣1)=2,
∴当t>0时,|f(t)+f(﹣t)|<f(t)﹣f(﹣t),|f(t)﹣f(﹣t)|=f(t)﹣f(﹣t),
故A错误,B错误;
当t>0时,令g(t)=f(1+t)+f(1﹣t)=(1+t)2+(1﹣t)3=﹣t3+4t2﹣t+2,
则g′(t)=﹣3t2+8t﹣1,令g′(t)=0得﹣3t2+8t﹣1=0,
∴△=64﹣12=52,∴g(t)有两个极值点t1,t2,
∴g(t)在(t2,+∞)上为减函数,
∴存在t0>t2,使得g(t0)<0,
∴|g(t0)|>g(t0),
故C正确;
令h(t)=(1+t)﹣f(1﹣t)=(1+t)2﹣(1﹣t)3=t3﹣2t2+5t,
则h′(t)=3t2﹣4t+5=3(t![]() )2
)2![]() 0,
0,
∴h(t)在(0,+∞)上为增函数,∴h(t)>h(0)=0,
∴|h(t)|=h(t),即|f(1+t)﹣f(1﹣t)|=f(1+t)﹣f(1﹣t),
故D错误.
故选:C.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,已知圆柱![]() ,底面半径为1,高为2,
,底面半径为1,高为2,![]() 是圆柱的一个轴截面,动点
是圆柱的一个轴截面,动点![]() 从点
从点![]() 出发沿着圆柱的侧面到达点
出发沿着圆柱的侧面到达点![]() ,其路径最短时在侧面留下的曲线记为
,其路径最短时在侧面留下的曲线记为![]() :将轴截面
:将轴截面![]() 绕着轴
绕着轴![]() ,逆时针旋转
,逆时针旋转![]()
![]() 角到
角到![]() 位置,边
位置,边![]() 与曲线
与曲线![]() 相交于点
相交于点![]() .
.
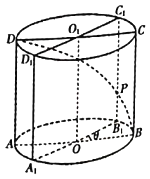
(1)当![]() 时,求证:直线
时,求证:直线![]() 平面
平面![]() ;
;
(2)当![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿基米德(公元前![]() 年—公元前
年—公元前![]() 年)不仅是著名的物理学家,也是著名的数学家,他利用“逼近法”得到椭圆的面积除以圆周率
年)不仅是著名的物理学家,也是著名的数学家,他利用“逼近法”得到椭圆的面积除以圆周率![]() 等于椭圆的长半轴与短半轴的乘积.已知平面直角坐标系
等于椭圆的长半轴与短半轴的乘积.已知平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]()
![]() 的面积为
的面积为![]() ,两焦点与短轴的一个顶点构成等边三角形.
,两焦点与短轴的一个顶点构成等边三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于不同的两点
交于不同的两点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率的调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除![]() 元后的余额为应纳税所得额,依照个人所得税税率表,调整前后的计算方法如下表:
元后的余额为应纳税所得额,依照个人所得税税率表,调整前后的计算方法如下表:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额 | 免征额 | ||||
级数 | 全月应纳税所得额 | 税率( | 级数 | 全月应纳税所得额 | 税率( |
1 | 不超过 |
| 1 | 不超过 |
|
2 | 超过 |
| 2 | 超过 |
|
3 | 超过 |
| 3 | 超过 |
|
… | … | … | … | … | … |
某税务部门在某公式利用分层抽样方法抽取2019年3月![]() 个不同层次员工的税前收入,并制成下面的频数分布表:
个不同层次员工的税前收入,并制成下面的频数分布表:
收入(元) |
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
(1)先从收入在![]() 及
及![]() 的人群中按分层抽样抽取
的人群中按分层抽样抽取![]() 人,则收入在
人,则收入在![]() 及
及![]() 的人群中分别抽取多少人?
的人群中分别抽取多少人?
(2)在从(1)中抽取的人中选![]() 人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率.
人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通![]() 座以下私家车投保交强险第一年的费用(基准保费)统一为
座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一年度未发生有责任道路交通事故 | 下浮 |
| 上两年度未发生有责任道路交通事故 | 下浮 |
| 上三年度未发生有责任道路交通事故 | 下浮 |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 |
|
| 上一个年度发生两次及两次以上有责任不涉及死亡的道路交通事故 | 上浮 |
| 上一个年度发生有责任交通死亡事故 | 上浮 |
某机构为了解某一品牌普通![]() 座以下私家车的投保情况,随机抽取了
座以下私家车的投保情况,随机抽取了![]() 辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
数量 |
|
|
|
|
|
以这![]() 辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定,![]() ,记
,记![]() 为某同学家的一辆该品牌车在第四年续保时的费用,求
为某同学家的一辆该品牌车在第四年续保时的费用,求![]() 的分布列与数学期望;(数学期望值保留到个位数字)
的分布列与数学期望;(数学期望值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损![]() 元,一辆非事故车盈利
元,一辆非事故车盈利![]() 元:
元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进![]() 辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】武汉市政府为了给“世界军运会”营造良好交通环境,特招聘了一批交通协管员,这些协管员的年龄都在![]() 之间,按年龄情况对他们进行统计得到的频率分布直方图如下,其中年龄在
之间,按年龄情况对他们进行统计得到的频率分布直方图如下,其中年龄在![]() 岁的有10人,
岁的有10人,![]() 岁的有45人.
岁的有45人.
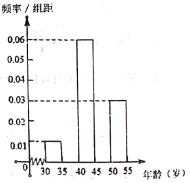
(1)补全频率分布直方图,并估计协管员的年龄中位数;
(2)为感谢年长的协管员的支持,利用分层抽样的方法从年龄在![]() 的协管员中抽取5人,并从这5人中再抽取3人,各赠送一份礼品,求仅有一人年龄在
的协管员中抽取5人,并从这5人中再抽取3人,各赠送一份礼品,求仅有一人年龄在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,汉诺塔问题是指有3根杆子A,B,C.B杆上有若干碟子,把所有碟子从B杆移到A杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面.把B杆上的4个碟子全部移到A杆上,最少需要移动( )次. ( )
A.12 B.15 C.17 D.19
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com