
【题目】设f(x)是二次函数,其图象过点(0,1),且在点(-2,f(-2))处的切线方程为2x+y+3=0
(1)求f(x)的表达式;
(2)求f(x)的图象与两坐标轴所围成图形的面积;
(3)若直线x=-t(0<t<1)把f(x)的图象与两坐标轴所围成图形的面积二等分,求t的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知A(x1 , f(x1),B(x2 , f(x2))是函数f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() <φ<0)图象上的任意两点,且初相φ的终边经过点P(1,﹣
<φ<0)图象上的任意两点,且初相φ的终边经过点P(1,﹣ ![]() ),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为
),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为 ![]() . (Ⅰ)求函数f(x)的解析式;
. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)当x∈[0, ![]() ]时,求函数f(x)的单调递增区间;
]时,求函数f(x)的单调递增区间;
(Ⅲ)当x∈[0, ![]() ]时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
]时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为一简单组合体,其底面ABCD为正方形,棱PD与EC均垂直于底面ABCD,PD=2EC,N为PB的中点,求证: 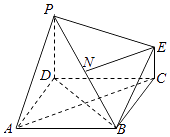
(1)平面EBC∥平面PDA;
(2)NE⊥平面PDB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点Pn(an , bn)满足an+1=an·bn+1 , bn+1=(n∈N*)且点P1的坐标为(1,-1).
(1)求过点P1 , P2的直线l的方程;
(2)试用数学归纳法证明:对于n∈N* , 点Pn都在(1)中的直线l上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+2﹣x . (Ⅰ)试写出这个函数的性质(不少于3条,不必说明理由),并作出图象;
(Ⅱ)设函数g(x)=4x+4﹣x﹣af(x),求这个函数的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,其中 n 为正整数.
,其中 n 为正整数.
(1)求f(1),f(2),f(3) 的值;
(2)猜想满足不等式 f(n)<0 的正整数 n 的范围,并用数学归纳法证明你的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果命题 p(n) 对 n=k 成立,那么它对 n=k+2 也成立,又若 p(n) 对 n=2 成立,则下列结论正确的是( )
A.p(n) 对所有自然数 n 成立
B.p(n) 对所有正偶数 n 成立
C.p(n) 对所有正奇数 n 成立
D.p(n) 对所有大于1的自然数 n 成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z=lg(m2﹣2m﹣2)+(m2+3m+2)i,根据以下条件分别求实数m的值或范围.
(1)z是纯虚数;
(2)z对应的点在复平面的第二象限.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com