
 若椭圆
若椭圆 (a>b>0)的左右焦点分别为F1,F2,线段F1F2被抛物线y2=2bx的焦点F内分成了3:1的两段.
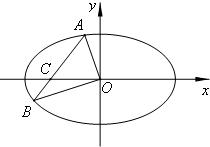
(a>b>0)的左右焦点分别为F1,F2,线段F1F2被抛物线y2=2bx的焦点F内分成了3:1的两段.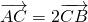 ,当△AOB的面积最大时,求直线l和椭圆的方程.
,当△AOB的面积最大时,求直线l和椭圆的方程. =3(c-
=3(c- ),…(2分)
),…(2分)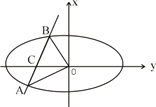 ∴e=
∴e= =
=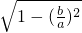 =
= .…(5分)
.…(5分)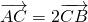 ,
, ,消去x,得(k2+2)y2-2ky+1-2b2=0,
,消去x,得(k2+2)y2-2ky+1-2b2=0,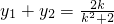 ,…②
,…②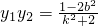 ,…③
,…③ ,
,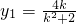 ,…(9分)
,…(9分)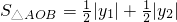 =
=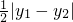 ,
,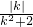 =3•
=3•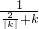 ≤3•
≤3•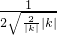 =
=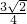 ,…(11分)
,…(11分) 时取等号,
时取等号,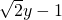 或x=
或x=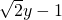 .…(12分)
.…(12分)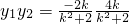 =-
=-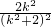 =-1,
=-1,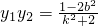 ,得b2=
,得b2= ,
,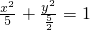 .…(14分)
.…(14分) =3(c-
=3(c- ),能够求出椭圆的离心率.
),能够求出椭圆的离心率.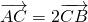 ,知2y2+y1=0,由
,知2y2+y1=0,由 ,得(k2+2)y2-2ky+1-2b2=0,再利用韦达定理,结合题设条件,能够求出椭圆方程.
,得(k2+2)y2-2ky+1-2b2=0,再利用韦达定理,结合题设条件,能够求出椭圆方程.

科目:高中数学 来源: 题型:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源:2011-2012年黑龙江省高二上学期期中考试文科数学 题型:解答题
若椭圆 =1(a>b>0)与直线
=1(a>b>0)与直线 在第一象限内有两个不同的交点,求a、b所满足的条件,并画出点P(a,b)的存在区域。
在第一象限内有两个不同的交点,求a、b所满足的条件,并画出点P(a,b)的存在区域。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com