
已知:0<a<b<c<d 且a+d=b+c,求证: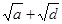 <
< 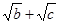
见解析
解析试题分析:
直接证明显然不容易入手,所以采用分析法证明,从要证明的不等式出发,寻找使这个不等式成立的某一"充分的"条件,为此逐步往前追溯(执果索因),一直追溯到已知条件或一些真命题为止.
根据题意可知, 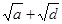 和
和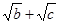 都是正数,所以为了证明结论,给不等式两边同时平方,而后根据题意
都是正数,所以为了证明结论,给不等式两边同时平方,而后根据题意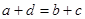 ,只需证明
,只需证明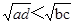 ,将其平方,可得
,将其平方,可得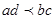 .由于不等式中含有四个未知数,所以可利用其中三个将另一个表示出来,不妨消掉
.由于不等式中含有四个未知数,所以可利用其中三个将另一个表示出来,不妨消掉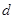 ,即
,即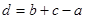 ,带入
,带入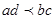 ,化简可得
,化简可得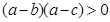 ,根据题意,
,根据题意,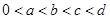 ,该不等式显然成立.所以该不等式得证.
,该不等式显然成立.所以该不等式得证.
试题解析:因为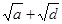 和
和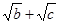 都是正数,
都是正数,
所以为了证明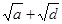 <
<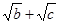
只需证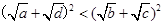
只需证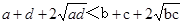
而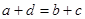
即证 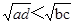
即证 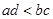
又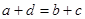 所以
所以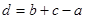
即证: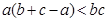
即证: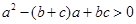
即证: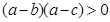
而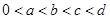
所以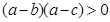 显然成立
显然成立
所以原不等式成立。
考点:分析法证明不等式.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com