
做一个无盖的圆柱形水桶,若要使体积是27π,且用料最省,则圆柱的底面半径为 .
3
【解析】
试题分析:设圆柱的高为h,半径为r则由圆柱的体积公式可得,πr2h=27π,即 ,要使用料最省即求全面积的最小值,而S全面积=πr2+2πrh=
,要使用料最省即求全面积的最小值,而S全面积=πr2+2πrh= =
=
(法一)令S=f(r),结合导数可判断函数f(r)的单调性,进而可求函数取得最小值时的半径
(法二):S全面积=πr2+2πrh= =
= ,利用基本不等式可求用料最小时的r
,利用基本不等式可求用料最小时的r
解:设圆柱的高为h,半径为r
则由圆柱的体积公式可得,πr2h=27π

S全面积=πr2+2πrh= =
=
(法一)令S=f(r),(r>0)
 =
=
令f′(r)≥0可得r≥3,令f′(r)<0可得0<r<3
∴f(r)在(0,3)单调递减,在[3,+∞)单调递增,则f(r)在r=3时取得最小值
(法二):S全面积=πr2+2πrh= =
=
=
 =27π
=27π
当且仅当 即r=3时取等号
即r=3时取等号
当半径为3时,S最小即用料最省
故答案为:3
点评:本题主要考查了圆柱的体积公式及表面积的最值的求解,解答应用试题的关键是要把实际问题转化为数学问题,根据已学知识进行解决.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
命题“所有能被5整除的数都是偶数”的否定形式是( )
A.所有不能被5整除的数都是偶数
B.所有能被5整除的数都不是偶数
C.存在一个不能被5整除的数都是偶数
D.存在一个能被5整除的数不是偶数
查看答案和解析>>
科目:高中数学 来源: 题型:
已知 分另为椭圆的上、下焦点,
分另为椭圆的上、下焦点, 是抛物线
是抛物线 的焦点,点
的焦点,点 是
是 与
与 在第二象限的交点, 且
在第二象限的交点, 且
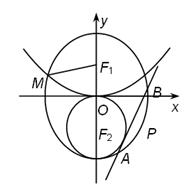
(1)求椭圆 的方程;
的方程;
(2)与圆 相切的直线
相切的直线 交椭圆
交椭圆 于
于 ,若椭圆
,若椭圆 上一点
上一点 满足
满足 ,求实数
,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
有如下四个结论:
①分别在两个平面内的两条直线一定是异面直线;
②过平面 的一条斜线有一个平面与平面
的一条斜线有一个平面与平面 垂直;
垂直;
③ “ ”是“
”是“ ”的必要条件;
”的必要条件;
④命题“ ”的否定是“
”的否定是“ ”.
”.
其中正确结论的个数为( )
A.4 B.3 C.2 D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com