
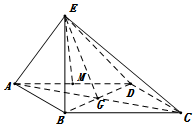
 如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.分析 (1)只需证明AC⊥BD,AC⊥BE,即可证明AC⊥平面BED,
(2)取AD中点为M,连接EM.设点G到平面AED的距离为为h,则
三棱锥E-ADG的体积为${V}_{E-ADG}=\frac{1}{3}×\frac{1}{2}×AG×DG×BE$=${V}_{G-ADE}=\frac{1}{3}×\frac{1}{2}×AD×EM×h$,
可求得点G到平面AED的距离
解答 解:(1)证明:因为四边形ABCD为菱形,
所以AC⊥BD,…(1分)
因为BE⊥平面ABCD,AC?平面ABCD,
所以AC⊥BE,…(2分)
又因为DB∩BE=B,所以AC⊥平面BED.…(3分)
又AC?平面AEC,所以平面AEC⊥平面BED.…(5分)
(2)取AD中点为M,连接EM.
因为∠ABC=120°.,AB=2,
所以AB=DB=2,AG=$\sqrt{3}$,DG=1,
因为AE⊥EC,所以EG=$\frac{1}{2}AC$=$\sqrt{3}$,所以BE=$\sqrt{2}$,…(6分)
所以AE=DE=$\sqrt{6}$,
又所以AD中点为M,所以EM⊥AD且EM=$\sqrt{5}$.设点G到平面AED的距离为为h,
则三棱锥E-ADG的体积为
V${V}_{E-ADG}=\frac{1}{3}×\frac{1}{2}×AG×DG×BE$=${V}_{G-ADE}=\frac{1}{3}×\frac{1}{2}×AD×EM×h$,
即$\frac{1}{3}×\frac{1}{2}×\sqrt{3}×1×\sqrt{2}=\frac{1}{3}×\frac{1}{2}×2×\sqrt{5}×h$,
解得h=$\frac{\sqrt{30}}{10}$.
所以点G到平面AED的距离为$\frac{\sqrt{30}}{10}$.…(10分)
点评 本题考查了空间线面垂直的判定,等体积法求点面距离.属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
 如图所示,在直角梯形ABEF中,将DCEF沿CD折起使∠FDA=60°,得到一个空间几何体.
如图所示,在直角梯形ABEF中,将DCEF沿CD折起使∠FDA=60°,得到一个空间几何体.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P | B. | Q | C. | {-1,1} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 广告费x/万元 | 4 | 2 | 3 | 5 |
| 销售额y/万元 | 49 | 26 | 39 | 54 |
| A. | 63.6万元 | B. | 65.5万元 | C. | 67.7万元 | D. | 72.0万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com