
 如图所示,在直角梯形ABEF中,将DCEF沿CD折起使∠FDA=60°,得到一个空间几何体.
如图所示,在直角梯形ABEF中,将DCEF沿CD折起使∠FDA=60°,得到一个空间几何体.分析 (1)由余弦定理求出AF=$\sqrt{3}$,由勾股定理得AF⊥AD,再由DC⊥FD,DC⊥AD,得DC⊥平面ADE,从而DC⊥AF,由此能证明AF⊥平面ABCD.
(2)由题意知DF=2,CE=1,AF=$\sqrt{3}$,BC⊥DC,BC=DC=1,E到平面ABCD的距离d=$\frac{1}{2}AF$,由此能求出三棱锥E-BCD的体积.
解答 证明:(1)由于∠FDA=60°,FD=2,AD=1,
∴AF2=FD2+AD2-2×FD×AD×cos∠FDA=4+1-2×2×1×$\frac{1}{2}$=3,
即AF=$\sqrt{3}$,∴AF2+AD2=FD2,∴AF⊥AD.
又∵DC⊥FD,DC⊥AD,AD∩FD=D,
AD,DF?平面ADF
∴DC⊥平面ADE,AF?平面ADF,
∴DC⊥AF,
∵AD∩DC=D,AD,DC?平面ABCD.
∴AF⊥平面ABCD.
解:(2)由题意知DF=2,CE=1,AF=$\sqrt{3}$,BC⊥DC,
BC=DC=1,
∴S△BDC=$\frac{1}{2}×1×1=\frac{1}{2}$,E到平面ABCD的距离d=$\frac{1}{2}AF$=$\frac{\sqrt{3}}{2}$,
∴三棱锥E-BCD的体积V=$\frac{1}{3}×{S}_{△BCD}×d$=$\frac{1}{3}×\frac{1}{2}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{12}$.
点评 本题考查线面垂直的证明,考查三棱锥的体积的求法,考查推理论证能力、运算求解能力、空间思维能力,考查转化化归思想、数形结合思想,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,从左到右有五个空格.
如图,从左到右有五个空格.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
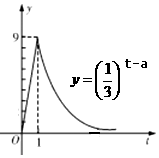 我国科研人员屠呦呦发现从青篙中提取的青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
我国科研人员屠呦呦发现从青篙中提取的青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{341}$ | B. | $\frac{32}{341}$ | C. | $\frac{64}{341}$ | D. | $\frac{128}{341}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com