
分析 由$\overrightarrow{AC}$=$\overrightarrow{BO}$,可得$\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{BO}$,再利用向量夹角公式即可得出.
解答 解:∵$\overrightarrow{AC}$=$\overrightarrow{BO}$,
∴$\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{BO}$=(2,3)-(-3,2)=(5,1),
∴$cos<\overrightarrow{OC},\overrightarrow{OB}>$=$\frac{\overrightarrow{OC}•\overrightarrow{OB}}{|\overrightarrow{OC}||\overrightarrow{OB}|}$=$\frac{-13}{\sqrt{26}×\sqrt{13}}$=-$\frac{\sqrt{2}}{2}$,
∴向量$\overrightarrow{OC}$与$\overrightarrow{OB}$的夹角为135°.
点评 本题考查了向量夹角公式、数量积运算性质、向量的坐标运算法则,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
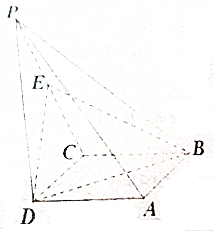 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠DBC=45°,$\frac{BD}{BC}$=$\sqrt{2}$,侧棱PD⊥底面ABCD,PD=CD,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠DBC=45°,$\frac{BD}{BC}$=$\sqrt{2}$,侧棱PD⊥底面ABCD,PD=CD,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com