

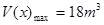 ,此时
,此时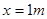 。
。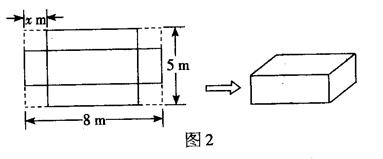
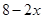 ,宽为
,宽为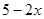 ,高为
,高为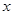
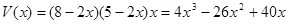 ……(4分)
……(4分)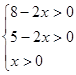 ,则0
,则0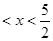 ……………(5分)
……………(5分)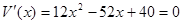
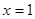 或
或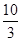 (舍)…………………………………………………(8分)
(舍)…………………………………………………(8分)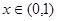 时,
时,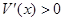 ;当
;当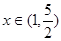 时,
时,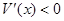 ………(10分)
………(10分)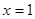 是V(x)的极大值点,也是
是V(x)的极大值点,也是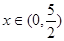 上的最大值点
上的最大值点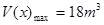 ,此时
,此时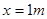 ……………………………………(12分)
……………………………………(12分)

科目:高中数学 来源:不详 题型:解答题
 图象上一点
图象上一点 处
处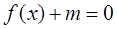 在
在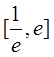 内有两个不等实根,求m的取值范围(其
内有两个不等实根,求m的取值范围(其 为自然对数的底数);
为自然对数的底数);查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 经过点
经过点 、
、 与
与 ,
, ,
, ,设函数
,设函数 在
在 和
和 处取到极值.
处取到极值. 表示
表示 ;
; 的大小(要求按从小到大排列);
的大小(要求按从小到大排列); ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线 均相切,求
均相切,求 的解析式.
的解析式.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 =
= (
(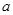 为实常数).
为实常数). 在
在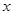 =1处与
=1处与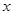 轴相切,求实数
轴相切,求实数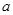 的值.
的值.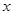 ∈[1,
∈[1, ],使得
],使得 ≤
≤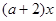 成立,求实数
成立,求实数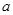 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
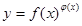 的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得 ,两边对
,两边对 求导数,得
求导数,得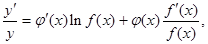 于是
于是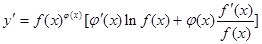 ,运用此方法可以求得函数
,运用此方法可以求得函数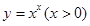 在(1,1)处的切线方程是 _________
在(1,1)处的切线方程是 _________查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com