
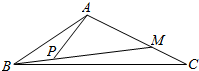
 如图,已知△ABC中,点M在线段AC上,点P在线段BM上且满足$\frac{AM}{MC}=\frac{MP}{PB}$=2,若$|\overrightarrow{AB}|$=2,$|\overrightarrow{AC}|$=3,∠BAC=120°,则$\overrightarrow{AP}•\overrightarrow{BC}$的值为( )
如图,已知△ABC中,点M在线段AC上,点P在线段BM上且满足$\frac{AM}{MC}=\frac{MP}{PB}$=2,若$|\overrightarrow{AB}|$=2,$|\overrightarrow{AC}|$=3,∠BAC=120°,则$\overrightarrow{AP}•\overrightarrow{BC}$的值为( )| A. | -2 | B. | 2 | C. | $\frac{2}{3}$ | D. | $-\frac{11}{3}$ |
分析 利用数量积运算性质可得:$\overrightarrow{AB}•\overrightarrow{AC}$.利用向量共线定理及其三角形法则可得$\overrightarrow{AP}$=$\frac{2}{3}\overrightarrow{AB}$+$\frac{2}{9}$$\overrightarrow{AC}$.再利用数量积运算性质即可得出.
解答 解:∵$|\overrightarrow{AB}|$=2,$|\overrightarrow{AC}|$=3,∠BAC=120°,∴$\overrightarrow{AB}•\overrightarrow{AC}$=2×3×cos120°=-3.
∵$\overrightarrow{MP}=\frac{2}{3}\overrightarrow{MB}$,∴$\overrightarrow{AP}-\overrightarrow{AM}$=$\frac{2}{3}(\overrightarrow{AB}-\overrightarrow{AM})$,化为$\overrightarrow{AP}$=$\frac{2}{3}\overrightarrow{AB}$+$\frac{1}{3}\overrightarrow{AM}$=$\frac{2}{3}\overrightarrow{AB}$+$\frac{1}{3}×\frac{2}{3}$$\overrightarrow{AC}$=$\frac{2}{3}\overrightarrow{AB}$+$\frac{2}{9}$$\overrightarrow{AC}$.
∴$\overrightarrow{AP}•\overrightarrow{BC}$=$(\frac{2}{3}\overrightarrow{AB}+\frac{2}{9}\overrightarrow{AC})$•$(\overrightarrow{AC}-\overrightarrow{AB})$=$\frac{4}{9}\overrightarrow{AB}•\overrightarrow{AC}$+$\frac{2}{9}{\overrightarrow{AC}}^{2}$-$\frac{2}{3}{\overrightarrow{AB}}^{2}$=$\frac{4}{9}×(-3)$+$\frac{2}{9}×{3}^{2}$-$\frac{2}{3}×{2}^{2}$=-2.
故选:A.
点评 本题考查了数量积运算性质、向量共线定理及其三角形法则,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | e | B. | $\frac{1}{e}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com