
已知圆C的圆心在直线l:3x-y=0上,且与直线l1:x-y+4=0相切.
(1)若直线x-y=0截圆C所得弦长为2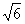 ,求圆C的方程.
,求圆C的方程.
(2)若圆C与圆x2+y2-4x-12y+8=0外切,试求圆C的半径.
(3)满足已知条件的圆显然不只一个,但它们都与直线l1相切,我们称l1是这些圆的公切线.这些圆是否还有其他公切线?若有,求出公切线的方程,若没有,说明理由.
设圆C的圆心坐标为(a,3a),则它的半径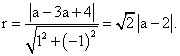
(1)圆心C到直线x-y=0的距离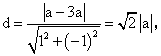
因而该直线截圆C所得弦长为
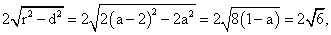
所以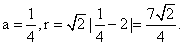
圆C的方程为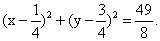
(2)两圆的连心线长为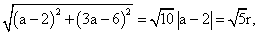 因为两圆外切,
因为两圆外切,
所以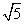 r=r+4
r=r+4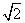 ,所以r=
,所以r=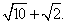
(3)如果存在另一条公切线,则它必过l与l1的交点(2,6).
①若斜率不存在,则其方程为x=2,圆心C到它的距离|a-2|=r=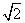 |a-2|,由于方程需要对任意的a都成立,因此无解,所以它不是公切线.
|a-2|,由于方程需要对任意的a都成立,因此无解,所以它不是公切线.
②若斜率存在,设公切线的方程为y-6=k(x-2),
即kx-y+6-2k=0,
所以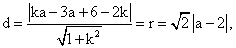
所以k2+6k-7=0,解出k=1或k=-7.
k=1时直线与l1重合,k=-7时,
直线方程为7x+y-20=0.
所以还存在一条公切线,其方程为7x+y-20=0.


科目:高中数学 来源: 题型:
已知直线x=2及x=4与函数y=log2x图象的交点分别为A,B,与函数y=lgx图象的交点分别为C,D,则直线AB与CD( )
(A)平行 (B)垂直 (C)不确定 (D)相交
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,若lg sin A-lg cos B-lg sin C=lg 2,则△ABC是( )
A.等腰三角形 B.直角三角形
C.等边三角形 D.等腰直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com