设t≠0,点P(t,0)是函数f(x)=x3+ax与g(x)=bx2+c的图象的一个公共点,两函数的图象在点P处有相同的切线.
(Ⅰ)用t表示a,b,c;
(Ⅱ)若函数y=f(x)-g(x)在(-1,3)上单调递减,求t的取值范围.
分析:(I)根据函数f(x),g(x)的图象都过点(t,0),以及f(x),g(x)在点(t,0)处有相同的切线,建立方程组,即可用t表示a,b,c;
(II)先利用导数求出y=f(x)-g(x)的单调减区间,然后使(-1,3)是单调减区间的子集,建立关系式,解之即可求出t的范围.
解答:解:(I)因为函数f(x),g(x)的图象都过点(t,0),所以f(t)=0,
即t
3+at=0.因为t≠0,所以a=-t
2.g(t)=0,即bt
2+c=0,所以c=ab.
又因为f(x),g(x)在点(t,0)处有相同的切线,所以f'(t)=g'(t).
而f'(x)=3x
2+a,g'(x)=2bx,所以3t
2+a=2bt.
将a=-t
2代入上式得b=t.因此c=ab=-t
3.故a=-t
2,b=t,c=-t
3.
(II)y=f(x)-g(x)=x
3-tx
2-t
2x+t
3,y'=3x
2-2tx-t
2=(3x+t)(x-t).
当y'=(3x+t)(x-t)<0时,函数y=f(x)-g(x)单调递减.
由y'<0,若t>0,则-
<x<t;若t<0,则t<x<-
.
由题意,函数y=f(x)-g(x)在(-1,3)上单调递减,则(-1,3)?(-
,t)或(-1,3)?(t,-
).
所以t≥3或-
≥3.即t≤-9或t≥3.
∴t的取值范围为(-∞,-9]∪[3,+∞).
点评:本题主要考查函数与导数的基本知识,几何意义及其应用,以及利用导数研究曲线上某点切线方程,同时考查学生数形结合思想以及转化与归化的能力,属于中档题.



 阅读快车系列答案
阅读快车系列答案 与
与 的图象的一个公共点,两函数的图象在点P处有相同的切线。
的图象的一个公共点,两函数的图象在点P处有相同的切线。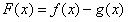 在(-1,3)上单调递减,求t的取值范围。
在(-1,3)上单调递减,求t的取值范围。