
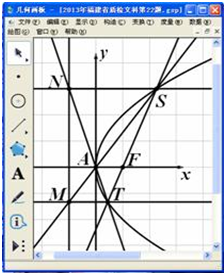
 ijͬѧ�á����λ��塷�о������ߵ����ʣ������λ��塷����������ij������E��y2=2px���������������⻭һ����S��������S�����꣨xS��yS������ͼ��
ijͬѧ�á����λ��塷�о������ߵ����ʣ������λ��塷����������ij������E��y2=2px���������������⻭һ����S��������S�����꣨xS��yS������ͼ������ ����xS=4��yS=4����y2=2px����p���������������E�ķ��̣�
������ֱ��l��my=x-1�����������߷��̣����M��N�����꣬�ɵ�$\overrightarrow{MT}$��$\overrightarrow{NS}$�����֤꣬��$\overrightarrow{MT}$��$\overrightarrow{NS}$�����ɵó����ۣ�
������������E��y2=4x�Ķ���ΪA������G��g��0����g��0��������G��ֱ��l��������E�ཻ��S��T���㣬ֱ��AS��AT�ֱ�ֱ��x=-g��M��N���㣬��MT��NS��
��� �⣺����xS=4��yS=4����y2=2px����p=2������3�֣�
��ˣ�������E�ķ���y2=4x������4�֣�
������Ϊ������E�Ľ���ΪF��1��0������S��x1��y1����T��x2��y2����
���������ֱ��l��my=x-1��
���������߷��̵�y2-4my-4=0��
��y1+y2=4m��y1y2=-4 �١���6�֣�
����ΪlAS��y=$\frac{{y}_{1}}{{x}_{1}}$•x��lAT��y=$\frac{{y}_{2}}{{x}_{2}}$•x��
����M��-1��-$\frac{{y}_{1}}{{x}_{1}}$����N��-1��-$\frac{{y}_{2}}{{x}_{2}}$����
����$\overrightarrow{MT}$=��x2+1��y2+$\frac{{y}_{1}}{{x}_{1}}$����$\overrightarrow{NS}$=��x1+1��y1+$\frac{{y}_{2}}{{x}_{2}}$��������7�֣�
����Ϊ��y2+$\frac{{y}_{1}}{{x}_{1}}$����x1+1��-��y1+$\frac{{y}_{2}}{{x}_{2}}$����x2+1��������8�֣�
=��y1-y2����$\frac{{{y}_{1}}^{2}{{y}_{2}}^{2}-16}{4{y}_{1}{y}_{2}}$������
�Ѣٴ���ڣ��ã�y1-y2����$\frac{{{y}_{1}}^{2}{{y}_{2}}^{2}-16}{4{y}_{1}{y}_{2}}$��=0������10�֣�
����y2+$\frac{{y}_{1}}{{x}_{1}}$����x1+1��-��y1+$\frac{{y}_{2}}{{x}_{2}}$����x2+1��=0��
����$\overrightarrow{MT}$��$\overrightarrow{NS}$��
����ΪM��T��N��S�ĵ㲻���ߣ�����MT��NS������11�֣�
������������E��y2=4x�Ķ���ΪA������G��g��0����g��0��������G��ֱ��l��������E�ཻ��S��T���㣬ֱ��AS��AT�ֱ�ֱ��x=-g��M��N���㣬��MT��NS������14�֣�
���� ��С����Ҫ���������ߵı����̡�ֱ����Բ���ߵ�λ�ù�ϵ�Ȼ���֪ʶ������������֤����������������������黯����ת��˼�롢����������˼�롢���ν��˼��ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com