
【题目】设函数f(x)=lg(x2+ax﹣a﹣1),给出下述命题:
①f(x)有最小值;
②当a=0时,f(x)的值域为R;
③若f(x)在区间[2,+∞)上单调递增,则实数a的取值范围是a≥﹣4;
④a=1时,f(x)的定义域为(﹣1,0);
则其中正确的命题的序号是
【答案】②
【解析】解:①f(x)有最小值不一定正确,因为定义域不是实数集时,
函数f(x)=lg(x2+ax﹣a﹣1)的值域是R,无最小值,
题目中不能排除这种情况的出现,故①不对.
②当a=0时,f(x)的值域为R是正确的,因为当a=0时,函数的定义域不是R,
即内层函数的值域是(0,+∞)故(x)的值域为R故②正确.
③若f(x)在区间[2,+∞)上单调递增,则实数a的取值范围是a≥﹣4.是不正确的,
由f(x)在区间[2,+∞)上单调递增,可得内层函数的对称轴﹣ ![]() ≤2,可得a≥﹣4,
≤2,可得a≥﹣4,
由对数式有意义可得4+2a﹣a﹣1>0,解得a>﹣3,
故由f(x)在区间[2,+∞)上单调递增,应得出a>﹣3,故③不对;
④a=1时,f(x)=lg(x2+x﹣2),令x2+x﹣2>0,解得:x>1或x<﹣2,
故函数的定义域是(﹣∞,﹣2)∪(1,+∞),故④不对;
综上,②正确,
所以答案是:②.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能正确解答此题.
上递减才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知p:关于x的不等式x2+2ax+4>0对一切 ![]() 恒成立;q:函数f(x)=-(5-2a)x在R上是减函数.若“p或q”为真,“p且q”为假,求实数a的取值范围( )。
恒成立;q:函数f(x)=-(5-2a)x在R上是减函数.若“p或q”为真,“p且q”为假,求实数a的取值范围( )。
A.![]()
B.B、
C.C、
D.a≥-2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列三个命题:
①若一个球的半径缩小到原来的 ![]() ,则其体积缩小到原来的
,则其体积缩小到原来的![]() ;
;
②若两组数据的平均数相等,则它们的标准差也相等;
③直线x+y+1=0与圆x2+y2= ![]() 相切.
相切.
其中真命题的序号是( )
A.①②③
B.①②
C.①③
D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga ![]() ,g(x)=1+loga(x﹣1),(a>0且a≠1),设f(x)和g(x)的定义域的公共部分为D,
,g(x)=1+loga(x﹣1),(a>0且a≠1),设f(x)和g(x)的定义域的公共部分为D,
(1)求集合D;
(2)当a>1时.若不等式g(x﹣ ![]() )﹣f(2x)>2在D内恒成立,求a的取值范围;
)﹣f(2x)>2在D内恒成立,求a的取值范围;
(3)是否存在实数a,当[m,n]D时,f(x)在[m,n]上的值域是[g(n),g(m)],若存在,求实数a的取值范围,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学将100名髙一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”

| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(I)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(II)根据频率分布直方图填写下面2 x2列联表,并判断是否有95%的把握认为:“成绩优秀”与教学方式有关.
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附: 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() ,在矩形ABCD中,
,在矩形ABCD中, ![]() ,
, ![]() ,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且
,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且![]() ,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由
,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由
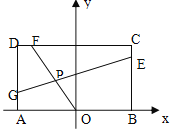
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com