
【题目】在四棱锥P﹣ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,AC∩BD=O. (Ⅰ)证明:PC⊥BD
(Ⅱ)若E是PA的中点,且△ABC与平面PAC所成的角的正切值为 ![]() ,求二面角A﹣EC﹣B的余弦值.
,求二面角A﹣EC﹣B的余弦值.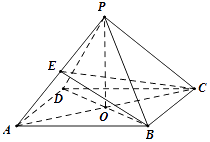
【答案】证明:(Ⅰ)因为底面是菱形,所以BD⊥AC. 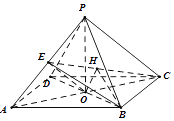
又PB=PD,且O是BD中点,所以BD⊥PO.
PO∩AC=O,所以BD⊥面PAC.
又PC面PAC,所以BD⊥PC.
(Ⅱ)由(Ⅰ)可知,OE是BE在面PAC上的射影,
所以∠OEB是BE与面PAC所成的角.
在Rt△BOE中, ![]() ,BO=1,所以
,BO=1,所以 ![]() .
.
在Rt△PEO中, ![]() ,
, ![]() ,所以
,所以 ![]() .
.
所以 ![]() ,又
,又 ![]() ,
,
所以PO2+AO2=PA2 , 所以PO⊥AO.
又PO⊥BD,BD∩AO=O,所以PO⊥面ABCD.
方法一:
过O做OH⊥EC于H,由(Ⅰ)知BD⊥面PAC,所以BD⊥EC,所以EC⊥面BOH,BH⊥EC,
所以∠OHB是二面角A﹣EC﹣B的平面角.
在△PAC中, ![]() ,所以PA2+PC2=AC2 , 即AP⊥PC.
,所以PA2+PC2=AC2 , 即AP⊥PC.
所以 ![]() .
.![]() ,得
,得 ![]() ,
, ![]() ,
, ![]() ,所以二面角A﹣EC﹣B的余弦值为
,所以二面角A﹣EC﹣B的余弦值为 ![]()
方法二:
如图,以 ![]() 建立空间直角坐标系,
建立空间直角坐标系,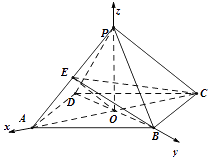
![]() ,B(0,1,0),
,B(0,1,0), ![]() ,
, ![]() ,
, 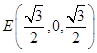 ,
, ![]() ,
, 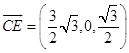 .
.
设面BEC的法向量为 ![]() ,则
,则  ,
,
即  ,得方程的一组解为
,得方程的一组解为 ![]() ,
,
即 ![]() .
.
又面AEC的一个法向量为 ![]() ,
,
所以  ,所以二面角A﹣EC﹣B的余弦值为
,所以二面角A﹣EC﹣B的余弦值为 ![]() .
.
【解析】(Ⅰ)证明BD⊥AC,BD⊥PO,推出BD⊥面PAC,然后证明BD⊥PC.(Ⅱ)说明OE是BE在面PAC上的射影,∠OEB是BE与面PAC所成的角.利用Rt△BOE,在Rt△PEO中,证明PO⊥AO.推出PO⊥面ABCD. 方法一:说明∠OHB是二面角A﹣EC﹣B的平面角.通过求解三角形求解二面角A﹣EC﹣B的余弦值.方法二:以 ![]() 建立空间直角坐标系,求出平面BEC的法向量,平面AEC的一个法向量,利用空间向量的数量积求解即可.
建立空间直角坐标系,求出平面BEC的法向量,平面AEC的一个法向量,利用空间向量的数量积求解即可.
【考点精析】根据题目的已知条件,利用直线与平面垂直的性质的相关知识可以得到问题的答案,需要掌握垂直于同一个平面的两条直线平行.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.若p:?x∈R,x2﹣x+1≥0,则¬p:?x∈R,x2﹣x+1<0
B.“ ![]() ”是“θ=30°或θ=150°”的充分不必要条件
”是“θ=30°或θ=150°”的充分不必要条件
C.命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0”
D.已知p:?x∈R,cosx=1,q:?x∈R,x2﹣x+2>0,则“p∧(¬q)”为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=e1﹣x(﹣a+cosx),a∈R.
(Ⅰ)若函数y=f(x)在[0,π]存在单调增区间,求实数a的取值范围;
(Ⅱ)若f( ![]() )=0,证明:对于x∈[﹣1,
)=0,证明:对于x∈[﹣1, ![]() ],总有f(﹣x﹣1)+2f′(x)cos(﹣x﹣1)>0.
],总有f(﹣x﹣1)+2f′(x)cos(﹣x﹣1)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1中,AA1=AB=AC=1,E,F分别是CC1 , BC的中点,AE⊥A1B1 , D为棱A1B1上的点. 
(1)证明:AB⊥AC;
(2)证明:DF⊥AE;
(3)是否存在一点D,使得平面DEF与平面ABC所成锐二面角的余弦值为 ![]() ?若存在,说明点D的位置,若不存在,说明理由.
?若存在,说明点D的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】体育课的排球发球项目考试的规则是:每位学生最多可发球3次,一旦发球成功,则停止发球,否则一直发到3次为止.设学生一次发球成功的概率为p (p≠0),发球次数为X,若X的数学期望EX>1.75,则p的取值范围是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.(0, ![]() )
)
D.( ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不恒为零的函数f(x)在定义域[0,1]上的图象连续不间断,满足条件f(0)=f(1)=0,且对任意x1 , x2∈[0,1]都有|f(x1)﹣f(x2)|≤ ![]() |x1﹣x2|,则对下列四个结论: ①若f(1﹣x)=f(x)且0≤x≤
|x1﹣x2|,则对下列四个结论: ①若f(1﹣x)=f(x)且0≤x≤ ![]() 时,f(x)=
时,f(x)= ![]() x(x﹣
x(x﹣ ![]() ),则当
),则当 ![]() <x≤1时,f(x)=
<x≤1时,f(x)= ![]() (1﹣x)(
(1﹣x)( ![]() ﹣x);
﹣x);
②若对x∈[0,1]都有f(1﹣x)=﹣f(x),则y=f(x)至少有3个零点;
③对x∈[0,1],|f(x)|≤ ![]() 恒成立;
恒成立;
④对x1 , x2∈[0,1],|f(x1)﹣f(x2)|≤ ![]() 恒成立.
恒成立.
其中正确的结论个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为 ![]() (α为参数).以点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ﹣
(α为参数).以点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ﹣ ![]() )=2
)=2 ![]() (Ⅰ)将直线l化为直角坐标方程;
(Ⅰ)将直线l化为直角坐标方程;
(Ⅱ)求曲线C上的一点Q 到直线l 的距离的最大值及此时点Q的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)=Asin(ωx+)(其中A>0,|φ| ![]() )的图象如图,为了得到
)的图象如图,为了得到 ![]() 的图象,则需将f(x)的图象( )
的图象,则需将f(x)的图象( ) 
A.向右平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向左平移 ![]() 个单位
个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com