
【题目】如图,![]() 是棱长为2的正方体,
是棱长为2的正方体,![]() 为面对角线
为面对角线![]() 上的动点(不包括端点),
上的动点(不包括端点),![]() 平面
平面![]() 交
交![]() 于点
于点![]() ,
,![]() 于
于![]() .
.

(1)试用反证法证明直线![]() 与
与![]() 是异面直线;
是异面直线;
(2)设![]() ,将
,将![]() 长表示为
长表示为![]() 的函数
的函数![]() ,并求此函数的值域;
,并求此函数的值域;
(3)当![]() 最小时,求异面直线
最小时,求异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
【答案】(1)证明见解析;(2)![]() ,值域
,值域![]() ;(3)
;(3)![]()
【解析】
(1)假设直线![]() 与
与![]() 是共面直线,利用公理2及长方体的相邻两个面不重合证明;
是共面直线,利用公理2及长方体的相邻两个面不重合证明;
(2)设![]() ,利用平行线解线段成比例求得
,利用平行线解线段成比例求得![]() ,得到
,得到![]() ,进一步求得
,进一步求得![]() ,再由勾股定理列式求解
,再由勾股定理列式求解![]() ,结合二次函数求值域;
,结合二次函数求值域;
(3)当![]() 时,
时,![]() 最小,此时
最小,此时![]() ,由于
,由于![]() ,又
,又![]() ,
,![]() 为异面直线
为异面直线![]() 与
与![]() 所成角的平面角,通过解直角三角形
所成角的平面角,通过解直角三角形![]() 得答案.
得答案.
(1)证明:假设直线![]() 与
与![]() 是共面直线,
是共面直线,
设直线![]() 与
与![]() 都在平面
都在平面![]() 上,则
上,则![]() 、
、![]() 、
、![]() 、
、![]() .
.
因此,平面![]() 、平面
、平面![]() 都与平面
都与平面![]() 有不共线的三个公共点,
有不共线的三个公共点,
即平面![]() 和平面
和平面![]() 重合(都与平面
重合(都与平面![]() 重合),
重合),
这与长方体的相邻两个面不重合矛盾,
于是,假设不成立,
![]() 直线
直线![]() 与
与![]() 是异面直线;
是异面直线;
(2)解:![]() 正方体
正方体![]() 的棱长为2,
的棱长为2,![]()
![]() ,
,
设![]() ,则
,则![]() ,得
,得![]() ,
,
![]() ,
,![]()
![]() ,得
,得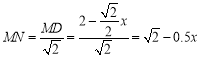 ,
,
![]()
![]()
![]()
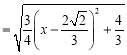 ,
,
当![]() 时,
时,![]() 有最小值为
有最小值为![]() ,当
,当![]() 时,
时,![]() ,
,
![]() 函数的值域为
函数的值域为![]() ;
;
(3)当![]() 时,
时,![]() 最小,此时
最小,此时![]() ,
,
在底面![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() 为异面直线
为异面直线![]() 与
与![]() 所成角的角,
所成角的角,
在![]() 中,
中,![]() 为直角,
为直角,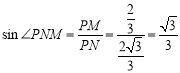 ,
,
![]() ,
,
∴异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.


科目:高中数学 来源: 题型:
【题目】产能利用率是指实际产出与生产能力的比率,工r产能利用率是衡量工业生产经营状况的重要指标.下图为国家统计局发布的2015年至2018年第2季度我国工业产能利用率的折线图.
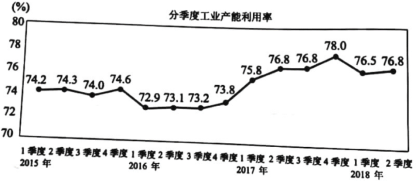
在统计学中,同比是指本期统计数据与上一年同期统计数据相比较,例如2016年第二季度与2015年第二季度相比较;环比是指本期统计数据与上期统计数据相比较,例如2015年第二季度与2015年第一季度相比较.
据上述信息,下列结论中正确的是( ).
A. 2015年第三季度环比有所提高B. 2016年第一季度同比有所提高
C. 2017年第三季度同比有所提高D. 2018年第一季度环比有所提高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机厂商在销售某型号手机时开展“手机碎屏险”活动.用户购买该型号手机时可选购“手机碎屏险”,保费为![]() 元,若在购机后一年内发生碎屏可免费更换一次屏幕,为了合理确定保费
元,若在购机后一年内发生碎屏可免费更换一次屏幕,为了合理确定保费![]() 的值,该手机厂商进行了问卷调查,统计后得到下表(其中
的值,该手机厂商进行了问卷调查,统计后得到下表(其中![]() 表示保费为
表示保费为![]() 元时愿意购买该“手机碎屏险”的用户比例):
元时愿意购买该“手机碎屏险”的用户比例):

(1)根据上面的数据计算得![]() ,求出
,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若愿意购买该“手机碎屏险”的用户比例超过![]() ,则手机厂商可以获利,现从表格中的
,则手机厂商可以获利,现从表格中的![]() 种保费任取
种保费任取![]() 种,求这
种,求这![]() 种保费至少有一种能使厂商获利的概率.
种保费至少有一种能使厂商获利的概率.
附:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某初级中学共有学生2000名,各年级男生女生人数如表: 已知在全校学生中随机抽取1名,抽到的是初二年级女生的概率是0.19.
初一年级 | 初二年级 | 初三年级 | |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
(1)求x的值.
(2)现用分层抽样法在全校抽取48名学生,问应在初三年级学生中抽取多少名?
(3)已知y≥245,z≥245,求初三年级女生比男生多的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)一个盒子里装有三张卡片,分别标记有数字![]() ,
,![]() ,
,![]() ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取![]() 次,每次抽取
次,每次抽取![]() 张,将抽取的卡片上的数字依次记为
张,将抽取的卡片上的数字依次记为![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求“抽取的卡片上的数字满足![]() ”的概率;
”的概率;
(Ⅱ)求“抽取的卡片上的数字![]() ,
,![]() ,
,![]() 不完全相同”的概率.
不完全相同”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某地区2008年至2014年中,每年的居民人均纯收入y(单位:千元)的数据如下表:
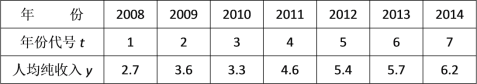
对变量t与y进行相关性检验,得知t与y之间具有线性相关关系.
(1)求y关于t的线性回归方程;
(2)预测该地区2016年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
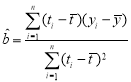 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信作为一款社交软件已经在支付,理财,交通,运动等各方面给人的生活带来各种各样的便利.手机微信中的“微信运动”,不仅可以看自己每天的运动步数,还可以看到朋友圈里好友的步数. ![]() 先生朋友圈里有大量好友使用了“微信运动”这项功能.他随机选取了其中40名,记录了他们某一天的走路步数,统计数据如下表所示:
先生朋友圈里有大量好友使用了“微信运动”这项功能.他随机选取了其中40名,记录了他们某一天的走路步数,统计数据如下表所示:

(1)以样本估计总体,视样本频率为概率,在![]() 先生的微信朋友圈里的男性好友中任意选取3名,其中走路步数不低于6000步的有
先生的微信朋友圈里的男性好友中任意选取3名,其中走路步数不低于6000步的有![]() 名,求
名,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)如果某人一天的走路步数不低于8000步,此人将被“微信运动”评定为“运动达人”,否则为“运动鸟人”.根据题意完成下面的![]() 列联表,并据此判断能否有90%以上的把握认为“评定类型”
列联表,并据此判断能否有90%以上的把握认为“评定类型”
与“性别”有关?

附:![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某艺术团组织的“微视频展示”活动中,该团体将从微视频的“点赞量”和“专家评分”两个角度来进行评优.若A视频的“点赞量”和“专家评分”中至少有一项高于B视频,则称A视频不亚于B视频.已知共有5部微视频展,如果某微视频不亚于其他4部视频,就称此视频为优秀视频.那么在这5部微视频中,最多可能有_______个优秀视频.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com