
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 通过椭圆方程确定交点A和B的坐标,利用两点间的距离公式求出AB的长,再根据三角形的面积求出AB边上的高,设出P的坐标,利用点到直线的距离公式表示出P到直线AB的距离即为AB边上的高,得到关于a和b的方程,把P代入椭圆方程得到关于a与b的另一个关系式,两者联立利用根的判别式判断出a与b的值有几对即可得到交点有几个.
解答 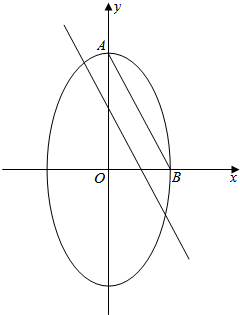 解:依题意,由对称性不妨设A(0,2),B(1,0),
解:依题意,由对称性不妨设A(0,2),B(1,0),
则直线AB方程为:y=-2x+2,|AB|=$\sqrt{(0-1)^{2}+(2-0)^{2}}$=$\sqrt{5}$,
∵△PAB的面积为$\frac{1}{2}$,即$\frac{1}{2}$|AB|•h=$\frac{1}{2}$,
∴AB边上的高h=$\frac{\sqrt{5}}{5}$,
设P的坐标为(a,b),则${a}^{2}+\frac{{b}^{2}}{4}=1$,点P到直线AB的距离d=$\frac{|2a+b-2|}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,
∴2a+b-2=1或2a+b-2=-1,
联立$\left\{\begin{array}{l}{2a+b=3}\\{{a}^{2}+\frac{{b}^{2}}{4}=1}\end{array}\right.$,消去b得:8a2-12a+5=0,
∵△=144-160=-16<0,∴方程无解;
联立$\left\{\begin{array}{l}{2a+b=1}\\{{a}^{2}+\frac{{b}^{2}}{4}=1}\end{array}\right.$,消去b得:8a2-4a-3=0,
∵△=16+96=112>0,
∴a有两个不相等的根,则对应的b也有两个不等的根;
综上所述,满足条件的P的个数有2个.
故选:B.
点评 考查学生会求直线与椭圆的交点坐标,灵活运用点到直线的距离公式化简求值,同时要求学生会利用根的判别式判断方程解的情况,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 若m⊥n,n?α,则m⊥α | B. | 若m∥α,n∥α,则m∥n | C. | 若m⊥α,n∥m,则n⊥α | D. | 若α⊥γ,β⊥γ,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
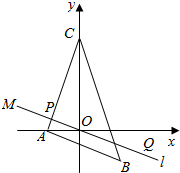 如图所示,已知A(-2,0),B(2,-2),C(0,5),过点M(-4,2)且平行于AB的直线l将△ABC分成两部分,求此两部分面积的比值.
如图所示,已知A(-2,0),B(2,-2),C(0,5),过点M(-4,2)且平行于AB的直线l将△ABC分成两部分,求此两部分面积的比值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{{x}^{2}}{x}$ | B. | y=($\sqrt{x}$)2 | C. | y=($\root{3}{x}$)3 | D. | y=|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com