Question

15．已知函数f（x）=|x-a|，g（x）=ax（a∈R）
（1）若函数y=f（x）的图象关于y轴对称，求出实数a的值；
（2）若方程f（x）=g（x）有两解，求实数a的取值范围；
（3）若a＞0，记F（x）=g（x）•f（x），求函数y=F（x） 在区间[1，2]上的最大值．

Answer 1

分析 （1）根据偶函数的定义即可求得a=0；
（2）根据绝对值的应用结合x的方程f（x）=g（x）有两解，即可求实数a的取值范围；
（3）求出h（x）=g（x）f（x）的表达式，运用分类讨论，并利用二次函数的性质，即可求函数y=h（x）在区间[1，2]上的最大值．

解答 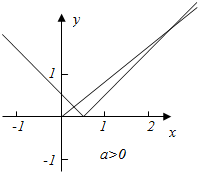解：（1）函数y=f（x）的图象关于y轴对称，即f（x）为偶函数，
f（-x）=f（x），即有|-x-a|=|x-a|，解得a=0；
（2）由|x-a|=ax，
若a=0，则方程等价为|x|=0，此时x=0，只有一个解，不满足条件．
若a＞0，分别作出函数y=|x-a|与y=ax的图象，
此时只要满足当x≥a时，y=|x-a|=x-a与y=ax有交点即可，
此时满足y=ax的斜率a＜1，即0＜a＜1，
若a＜0，只要满足当x≤a时，y=|x-a|=-x+a与y=ax有交点即可，
此时满足y=ax的斜率a＞-1，即-1＜a＜0，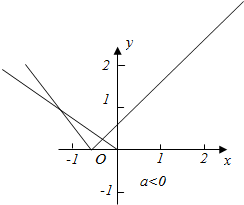
综上0＜a＜1或-1＜a＜0．
（3）h（x）=g（x）f（x）=|x-a|•ax=$\left\{\begin{array}{l}{a（{x}^{2}-ax），x≥a}\\{a（ax-{x}^{2}），x＜a}\end{array}\right.$
=$\left\{\begin{array}{l}{a[（x-\frac{a}{2}）^{2}-\frac{{a}^{2}}{4}]，x≥a}\\{a[-（x-\frac{a}{2}）^{2}+\frac{{a}^{2}}{4}]，x＜a}\end{array}\right.$，
当0＜a≤1时，f（x）在[1，2]上递增，h（x）在[1，2]递增，
h（x）_max=h（2）=2a（2-a）；
当1＜a$\frac{5}{3}$时，f（x）在[1，a]上递减，[a，2]递增，
h（1）-h（2）=a|1-a|-2a|a-2|=a（1-a）-2a（2-a）=a（3a-5）＜0，
即有h（x）_max=h（2）=2a（2-a）；
当$\frac{5}{3}$＜a＜2时，f（x）在[1，a]上递减，在[a，2]上递增，
h（1）-h（2）=3a-5＞0，h（1）＞h（2），
h（x）_max=h（1）=a（a-1）；
当2≤a≤4时，h_max（x）=F（$\frac{a}{2}$）=$\frac{{a}^{3}}{4}$，
当a＞4时，h_max（x）=h（2）=2a（a-2）．
综上可得h_max（x）$\left\{\begin{array}{l}{2a（2-a），0＜a≤\frac{5}{3}}\\{a（a-1），\frac{5}{3}＜a＜2}\\{\frac{{a}^{3}}{4}，2≤a≤4}\\{2a（a-2），a＞4}\end{array}\right.$．

点评 本题主要考查函数奇偶性和函数最值的求解，根据函数的奇偶性的定义以及一元二次函数的性质是解决本题的关键．