练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知直线l与两坐标轴围成的三角形的面积为3，分别求满足下列条件的直线l的方程：(1)过定点A(－3,4)；(2)斜率为.


    解：(1)设直线l的方程是y＝k(x＋3)＋4，

    它在x轴、y轴上的截距分别是－－3,3k＋4，

    由已知，得|(3k＋4)(－－3)|＝6，

    解得k1＝－或k2＝－.

    所以直线l的方程为2x＋3y－6＝0或8x＋3y＋12＝0.

    (2)设直线l在y轴上的截距为b，

    则直线l的方程是y＝x＋b，它在x轴上的截距是－6b，

    由已知，得|－6b·b|＝6，∴b＝±1.

    ∴直线l的方程为x－6y＋6＝0或x－6y－6＝0.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


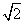    如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB＝，AF＝1，M是线段EF的中点．

    (1)求证：AM∥平面BDE；

    (2)试在线段AC上确定一点P，使得PF与CD所成的角是60°.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图如图，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为a，视力在4.6到5.0之间的学生数为b，则a，b的值分别为(　　)

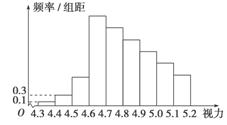
    A．0.27,78                        B．0.27,83

    C．2.7,78                         D．2.7,83

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某市居民2008～2012年家庭年平均收入x(单位：万元)与年平均支出Y(单位：万元)的统计资料如下表所示：

    年份

    2008

    2009

    2010

    2011

    2012

    收入x

    11.5

    12.1

    13

    13.3

    15

    支出Y

    6.8

    8.8

    9.8

    10

    12

    根据统计资料，居民家庭年平均收入的中位数是　　　，家庭年平均收入与年平均支出有__________线性相关关系．(第二个空填“正”或“负”)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    直线x＋a2y－a＝0(a＞0，a是常数)，当此直线在x，y轴上的截距和最小时，a的值是(　　)

    A．1                               B．2

    C.                              D．0

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    直线l过点P(－2,1)且斜率为k(k>1)，将直线l绕P点按逆时针方向旋转45°得到直线m，若直线l和m分别和y轴交于Q、R两点．

    (1)用k表示直线m的斜率；

    (2)当k为何值时，△PQR的面积最小，并求面积最小时直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知直线：l1：x＋ysinθ－1＝0，l2：2xsin θ＋y＋1＝0，若l1∥l2，则θ＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    根据下列条件，求圆的方程：

    (1)经过P(－2,4)、Q(3，－1)两点，并且在x轴上截得的弦长等于6；

    (2)圆心在直线y＝－4x上，且与直线l：x＋y－1＝0相切于点P(3，－2)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设F1，F2是椭圆E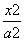：＋＝1(a＞b＞0)的左、右焦点，P为直线x＝上一点，△F2PF1是底角为30°的等腰三角形，则E的离心率为(　　)

    A.                               B.

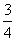    C.                               D.

    查看答案和解析>>

    同步练习册答案