

 与价格
与价格 之间有较好的线性相关关系,其线性回归直线方程是;
之间有较好的线性相关关系,其线性回归直线方程是;
 的值;
的值;科目:高中数学 来源:不详 题型:解答题
| | 总成绩好 | 总成绩不好 | 总计 |
| 数学成绩好 | 20 | 10 | 30 |
| 数学成绩不好 | 5 | 15 | 20 |
| 总计 | 25 | 25 | 50 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
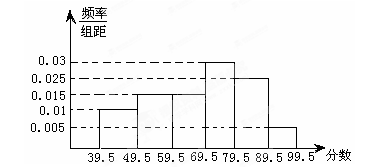
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.9 | B.8 | C.7 | D.6 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
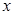 与数学成绩
与数学成绩 进行数据收集如下:
进行数据收集如下:| x | 15 | 16 | 18 | 19 | 22 |
| y | 102 | 98 | 115 | 115 | 120 |
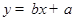 ,则点
,则点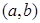 与直线
与直线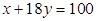 的位置关系是( )
的位置关系是( )查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | 嗜酒 | 不嗜酒 | 总计 |
| 患肝病 | 7 775 | 42 | 7 817 |
| 未患肝病 | 2 099 | 49 | 2 148 |
| 总计 | 9 874 | 91 | 9 965 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com