已知定义在R上的函数f(x)=ax3-2ax2+b(a>0)在区间[-2,1]上的最大值是5,最小值是-11.
(1)求函数f(x)的解析式;
(2)求曲线y=f(x)在x=-1处的切线方程;
(3)若t∈[-1,1]时,f′(x)+tx≤0恒成立,求实数x的取值范围.
解:(1)∵f(x)=ax
3-2ax
2+b,∴f
′(x)=3ax
2-4ax=ax(3x-4)
令f
′(x)=0解得x
1=0,

∉[-2,1](舍去)
由于a>0,f(x)在x∈[-2,0]上单调递增,在x∈[0,1]上单调递减,
∴f(0)必为最大值,而f(0)=5,因此b=5
由a>0,∴-a+b>-16a+b,即f(1)>f(-2)
则有f(x)
min=f(-2)=-16a+b=-16a+5=-11,∴a=1
∴f(x)=x
3-2x
2+5
(2)由(1)及题意得,f(-1)=2且f
′(x)=3x
2-4x
∴曲线在x=-1处的切线斜率k=f
′(-1)=3(-1)
2-4(-1)=7
∴曲线在x=-1处的切线方程为y-2=7(x+1),即7x-y+9=0
(3)由(2)及题意得f′(x)+tx≤0等价于3x
2-4x+tx≤0
令g(t)=xt+3x
2-4x
则所求问题等价于g(t)≤0在∈[-1,1]上恒成立求x的取值范围,
为此只需
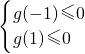
即

解得0≤x≤1.
故所求是实数x的取值范围为[0,1]
分析:(1)由导函数f
′(x)=3ax
2-4ax=ax(3x-4)即a>0可知f(x)在x∈[-2,0]上单调递增,在x∈[0,1]上单调递减,可知f(0)=5,f(-2)=-11,可解ab的值,解析式可求;
(2)由(1)可求x=-1处的斜率,可写方程;
(3)构造关于t的函数,则所求问题等价于g(t)≤0在∈[-1,1]上恒成立求x的取值范围,解方程组即可.
点评:本题为函数导数的综合应用,正确表示出函数在闭区间的最值是解决问题的关键,属中档题.

 ∉[-2,1](舍去)
∉[-2,1](舍去)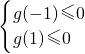 即
即 解得0≤x≤1.
解得0≤x≤1.

 名校课堂系列答案
名校课堂系列答案