
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是边长为2的正方形,侧面
是边长为2的正方形,侧面![]() 底面
底面![]() ,
,![]() 为
为![]() 上的点,且
上的点,且![]() 平面
平面![]()
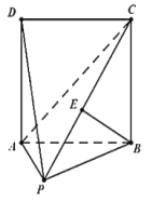
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 体积最大时,求二面角
体积最大时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见证明;(2)![]() .
.
【解析】
(1)通过侧面![]() 底面
底面![]() ,可以证明出
,可以证明出![]() 面
面![]() ,这样可以证明出
,这样可以证明出
![]() ,再利用
,再利用![]() 平面
平面![]() ,可以证明出
,可以证明出![]() ,这样利用线面垂直的判定定理可以证明出
,这样利用线面垂直的判定定理可以证明出![]() 面
面![]() ,最后利用面面垂直的判定定理可以证明出平面
,最后利用面面垂直的判定定理可以证明出平面![]() 平面
平面![]() ;
;
(2)利用三棱锥体积公式可得![]() ,
,
利用基本不等式可以求出三棱锥![]() 体积最大值,此时可以求出
体积最大值,此时可以求出![]() 的长度,以点
的长度,以点![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() 和
和![]() 分别作为
分别作为![]() 轴,
轴,![]() 轴和
轴和![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .求出相应点的坐标,求出面
.求出相应点的坐标,求出面![]() 的一个法向量,面
的一个法向量,面![]() 的一个法向量,利用空间向量数量积的运算公式,可以求出二面角
的一个法向量,利用空间向量数量积的运算公式,可以求出二面角![]() 的余弦值.
的余弦值.
(1)证明:∵侧面![]() 底面
底面![]() ,侧面
,侧面![]() 底面
底面![]() ,四边形
,四边形![]() 为正方形,∴
为正方形,∴![]() ,
,![]() 面
面![]() ,
,
∴![]() 面
面![]() ,
,
又![]() 面
面![]() ,
,
∴![]() ,
,
![]() 平面
平面![]() ,
,![]() 面
面![]() ,
,
∴![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 面
面![]() ,
,
![]() 面
面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)![]() ,
,
求三棱锥![]() 体积的最大值,只需求
体积的最大值,只需求![]() 的最大值.
的最大值.
令![]() ,由(1)知,
,由(1)知,![]() ,
,
∴![]() ,
,
而![]() ,
,
当且仅当![]() ,即
,即![]() 时,
时,
![]() 的最大值为
的最大值为![]() .
.
如图所示,分别取线段![]() ,
,![]() 中点
中点![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,
,
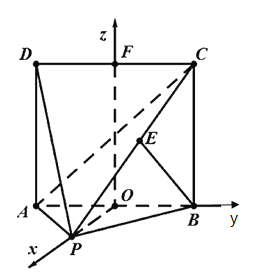
以点![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() 和
和![]() 分别作为
分别作为![]() 轴,
轴,![]() 轴和
轴和![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .
.
由已知![]() ,
,
所以![]() ,
,
令![]() 为面
为面![]() 的一个法向量,
的一个法向量,
则有![]() ,
,
∴![]()
易知![]() 为面
为面![]() 的一个法向量,
的一个法向量,
二面角![]() 的平面角为
的平面角为![]() ,
,![]() 为锐角
为锐角
则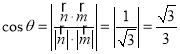 .
.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底而ABCD是菱形,且PA=AD=2,∠PAD=∠BAD=120°,E,F分别为PD,BD的中点,且![]() .
.
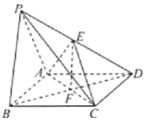
(1)求证:平面PAD⊥平面ABCD;
(2)求锐二面角E-AC-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】矩形ABCD中,![]() ,沿对角线AC将三角形ADC折起,得到四面体
,沿对角线AC将三角形ADC折起,得到四面体![]() ,四面体
,四面体![]() 外接球表面积为
外接球表面积为![]() ,当四面体
,当四面体![]() 的体积取最大值时,四面体
的体积取最大值时,四面体![]() 的表面积为( )
的表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨.销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.
(1)列出甲、乙两种产品满足的关系式,并画出相应的平面区域;
(2)在一个生产周期内该企业生产甲、乙两种产品各多少吨时可获得利润最大,最大利润是多少?
(用线性规划求解要画出规范的图形及具体的解答过程)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》是央视推出的一档以“赏中华诗词,寻文化基因,品生活之美”为宗旨的大型文化类竞赛节目,邀请全国各个年龄段、各个领域的诗词爱好者共同参与诗词知识比拼。“百人团”由一百多位来自全国各地的选手组成,成员上至古稀老人,下至垂髫小儿,人数按照年龄分组统计如下表:
分组(年龄) |
|
|
|
频数(人) |
|
|
|
(1)用分层抽样的方法从“百人团”中抽取![]() 人参加挑战,求从这三个不同年龄组中分别抽取的挑战者的人数;
人参加挑战,求从这三个不同年龄组中分别抽取的挑战者的人数;
(2)在(1)中抽出的![]() 人中,任选
人中,任选![]() 人参加一对一的对抗比赛,求这
人参加一对一的对抗比赛,求这![]() 人来自同一年龄组的概率。
人来自同一年龄组的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长均相等的四棱锥![]() 中,
中, ![]() 为底面正方形的中心,
为底面正方形的中心, ![]() ,
,![]() 分别为侧棱
分别为侧棱![]() ,
,![]() 的中点,有下列结论正确的有:( )
的中点,有下列结论正确的有:( )
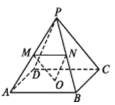
A.![]() ∥平面
∥平面![]() B.平面
B.平面![]() ∥平面
∥平面![]()
C.直线![]() 与直线
与直线![]() 所成角的大小为
所成角的大小为![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某学校研究性课题《什么样的活动最能促进同学们进行垃圾分类》向题的统计图(每个受访者都只能在问卷的5个活动中选择一个),以下结论错误的是( )

A. 回答该问卷的总人数不可能是100个
B. 回答该问卷的受访者中,选择“设置分类明确的垃圾桶”的人数最多
C. 回答该问卷的受访者中,选择“学校团委会宣传”的人数最少
D. 回答该问卷的受访者中,选择“公益广告”的人数比选择“学校要求”的少8个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com