
 ,乙班三名同学答对的概率分别是
,乙班三名同学答对的概率分别是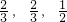 ,且这六名同学答题正确与否相互之间没有影响.
,且这六名同学答题正确与否相互之间没有影响.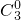 (1-
(1- )3=
)3= ,P(X=10)=
,P(X=10)=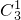 (1-
(1- )2=
)2= ,
,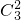 (
( )2(1-
)2(1- )=
)= ,P(X=30)=
,P(X=30)=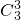 (
( )3=
)3=
| X | 0 | 10 | 20 | 30 |
| P |  |  |  |  |
 +10×
+10× +20×
+20× +30×
+30× =20.…5分
=20.…5分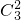 (
( )2(1-
)2(1- )×[
)×[ ×(1-
×(1- )×(1-
)×(1- )+(1-
)+(1- )×
)× ×(1-
×(1- )+(1-
)+(1- )×(1-
)×(1- )×
)× ]=
]= ;
;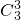 (
( )3×(1-
)3×(1- )×(1-
)×(1- )×(1-
)×(1- )=
)= .
. +
+ =
= . …10分
. …10分

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图是甲,乙两组各6名同学身高(单位:cm)数据的茎叶图.记甲,乙两组数据的平均数依次为
如图是甲,乙两组各6名同学身高(单位:cm)数据的茎叶图.记甲,乙两组数据的平均数依次为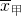 和
和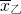 ,则
,则 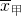 ________
________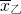 . (填入:“>”,“=”,或“<”)
. (填入:“>”,“=”,或“<”)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com