
【题目】如图,在三棱柱ABC﹣A1B1C1中,面ABB1A1为矩形,AB=1,AA1= ![]() ,D为AA1的中点,BD与AB1交于点O,CO⊥面ABB1A1
,D为AA1的中点,BD与AB1交于点O,CO⊥面ABB1A1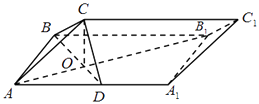
(Ⅰ)证明:BC⊥AB1
(Ⅱ)若OC=OA,求二面角A﹣BC﹣B1的余弦值.
【答案】(Ⅰ)证明:由△AB1B与△DBA相似,知DB⊥AB1,
又CD⊥平面ABB1A1,∴CD⊥AB1,
∴AB1⊥平面BDC,∴AB1⊥BC.
(Ⅱ)解:以O为坐标原点,OA、OD、OC所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,

则A( ![]() ,0,0),B(0,﹣
,0,0),B(0,﹣ ![]() ,0),C(0,0,
,0),C(0,0, ![]() ),B1(﹣
),B1(﹣ ![]() ,0,0),
,0,0),
![]() =(0,
=(0, ![]() ,
, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,﹣
,﹣ ![]() ,0),
,0), ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,0),
,0),
设平面ABC,平面BCB1的法向量分别为 ![]() ,
,
则  ,取x=
,取x= ![]() ,得
,得 ![]() =(
=( ![]() ),
),
 ,取a=1,得
,取a=1,得 ![]() =(1,
=(1, ![]() ,﹣2),
,﹣2),
∴cos< ![]() >=
>= ![]() =
= ![]() ,
,
∴二面角A﹣BC﹣B1的余弦值为﹣ ![]() .
.
【解析】(Ⅰ)推导出DB⊥AB1,CD⊥AB1,从而AB1⊥平面BDC,由此能证明AB1⊥BC.(Ⅱ)以O为坐标原点,OA、OD、OC所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出二面角A﹣BC﹣B1的余弦值.
【考点精析】认真审题,首先需要了解空间中直线与直线之间的位置关系(相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】定义在R上的函数y=f(x),恒有f(x)=f(2﹣x)成立,且f′(x)(x﹣1)>0,对任意的x1<x2 , 则f(x1)<f(x2)成立的充要条件是( )
A.x2>x1≥1
B.x1+x2>2
C.x1+x2≤2
D.x2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m≠0,向量 ![]() =(m,3m),向量
=(m,3m),向量 ![]() =(m+1,6),集合A={x|(x﹣m2)(x+m﹣2)=0}.
=(m+1,6),集合A={x|(x﹣m2)(x+m﹣2)=0}.
(1)判断“ ![]() ∥
∥ ![]() ”是“|
”是“| ![]() |=
|= ![]() ”的什么条件
”的什么条件
(2)设命题p:若 ![]() ⊥
⊥ ![]() ,则m=﹣19,命题q:若集合A的子集个数为2,则m=1,判断p∨q,p∧q,¬q的真假,并说明理由.
,则m=﹣19,命题q:若集合A的子集个数为2,则m=1,判断p∨q,p∧q,¬q的真假,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式ax2﹣x+b≥0的解集为[﹣2,1],则关于x的不等式bx2﹣x+a≤0的解集为( )
A.[﹣1,2]
B.[﹣1,![]() ]
]
C.[﹣![]() , 1]
, 1]
D.[﹣1,﹣![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤200时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=xv(x)可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数是( ) ①若f(x)= ![]() +a为奇函数,则a=
+a为奇函数,则a= ![]() ;
;
②“在△ABC中,若sinA>sinB,则A>B”的逆命题是假命题;
③“三个数a,b,c成等比数列”是“b= ![]() ”的既不充分也不必要条件;
”的既不充分也不必要条件;
④命题“x∈R,x3﹣x2+1≤0”的否定是“x0∈R,x03﹣x02+1>0”.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C: ![]() =1(a>b>0)的焦点F1 , F2 , 过右焦点F2的直线l与C相交于P、Q两点,若△PQF1的周长为短轴长的2
=1(a>b>0)的焦点F1 , F2 , 过右焦点F2的直线l与C相交于P、Q两点,若△PQF1的周长为短轴长的2 ![]() 倍.
倍.
(Ⅰ)求C的离心率;
(Ⅱ)设l的斜率为1,在C上是否存在一点M,使得 ![]() ?若存在,求出点M的坐标;若不存在,说明理由.
?若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+2a)﹣ax,a>0.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)记f(x)的最大值为M(a),若a2>a1>0且M(a1)=M(a2),求证: ![]() ;
;
(Ⅲ)若a>2,记集合{x|f(x)=0}中的最小元素为x0 , 设函数g(x)=|f(x)|+x,求证:x0是g(x)的极小值点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com