
【题目】在平面直角坐标系xOy中,以点(0,1)为圆心且与直线mx﹣y﹣2m﹣1=0(x∈R)相切的所有圆中,半径最大的圆的标准方程为 .
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,面ABB1A1为矩形,AB=1,AA1= ![]() ,D为AA1的中点,BD与AB1交于点O,CO⊥面ABB1A1
,D为AA1的中点,BD与AB1交于点O,CO⊥面ABB1A1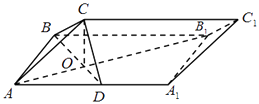
(Ⅰ)证明:BC⊥AB1
(Ⅱ)若OC=OA,求二面角A﹣BC﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax,g(x)= ![]() +a.
+a.
(1)当a=2 时,求F(x)=f(x)﹣g(x)在(0,2]的最大值;
(2)讨论函数F(x)=f(x)﹣g(x) 的单调性;
(3)若f(x)g(x)≤0 在定义域内恒成立,求实数a的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,3,则输出v的值为( ) 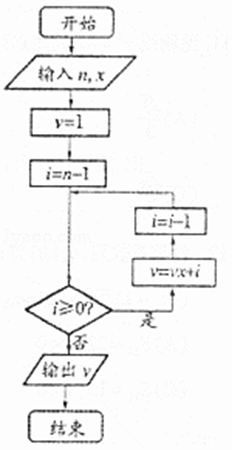
A.16
B.18
C.48
D.143
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1(﹣1,0),F2(1,0),曲线C1上任意一点M满足 ![]() ;曲线C2上的点N在y轴的右边且N到F2的距离与它到y轴的距离的差为1.
;曲线C2上的点N在y轴的右边且N到F2的距离与它到y轴的距离的差为1.
(1)求C1 , C2的方程;
(2)过F1的直线l与C1相交于点A,B,直线AF2 , BF2分别与C2相交于点C,D和E,F.求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A是双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左顶点,F1 , F2分别为左、右焦点,P为双曲线上一点,G是△F1PF2的重心,若
=1(a>0,b>0)的左顶点,F1 , F2分别为左、右焦点,P为双曲线上一点,G是△F1PF2的重心,若 ![]() =λ
=λ ![]() ,|
,| ![]() |=
|= ![]() ,|
,| ![]() |+|
|+| ![]() |=8,则双曲线的标准方程为( )
|=8,则双曲线的标准方程为( )
A.x2﹣ ![]() =1
=1
B.![]() ﹣y2=1
﹣y2=1
C.![]() =1
=1
D.x2﹣ ![]() =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】习大大构建的“一带一路”经济带的发展规划已经得到了越来越多相关国家的重视和参与.某市顺潮流、乘东风,闻迅而动,决定利用旅游资源优势,撸起袖子大干一场.为了了解游客的情况,以便制定相应的策略.在某月中随机抽取甲、乙两个景点各10天的游客数,画出茎叶图如下: 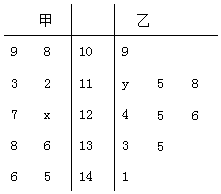
(1)若景点甲中的数据的中位数是125,景点乙中的数据的平均数是124,求x,y的值;
(2)若将图中景点甲中的数据作为该景点较长一段时期内的样本数据.今从这段时期中任取4天,记其中游客数超过120人的天数为ξ,求概率P(ξ≤2);
(3)现从上图的共20天的数据中任取2天的数据(甲、乙两景点中各取1天),记其中游客数不低于115且不高于125人的天数为η,求η的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E﹣ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DF的中点. (I)求证:BE∥平面ACF;
(II)求平面BCF与平面BEF所成锐二面角的余弦角.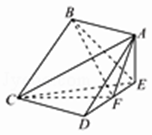
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com