
【题目】如图,在三棱柱![]() 中,每个侧面均为正方形,
中,每个侧面均为正方形, ![]() 为底边
为底边![]() 的中点,
的中点, ![]() 为侧棱
为侧棱![]() 上的点,且满足
上的点,且满足![]() 平面
平面![]() .
.
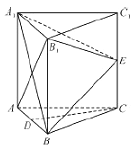
(1)求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析: (1)因为三棱柱各侧面都是正方形,所以![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]() ,可证
,可证![]() 平面
平面![]() ,,再利用直线与平面垂直的判定定理进行证明;
,,再利用直线与平面垂直的判定定理进行证明;
(2) 取![]() 中点
中点![]() ,连接
,连接![]() ,
, ![]() ,易知侧面
,易知侧面![]() 底面
底面![]() ,
,![]() 是
是![]() 与平面
与平面![]() 所成角.,然后构造直角三角形,在直角三角形中求其正弦值,从而求解.
所成角.,然后构造直角三角形,在直角三角形中求其正弦值,从而求解.
试题解析:(1)设![]() 和
和![]() 的交点为
的交点为![]() ,连接
,连接![]() ,
, ![]() ,
,
∵![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,
的中点,
∴![]() 又
又![]() ,∴
,∴![]() 即
即![]() ,
,
∵![]() 平面
平面![]() ,又平面
,又平面![]() 平面
平面![]() ,
,
∴![]() ,∴
,∴![]() 为
为![]() 的中点,
的中点,
∵三棱柱各侧面都是正方形,所以![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
由已知得![]() ,∴
,∴![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
∵侧面是正方形,∴![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)取![]() 中点
中点![]() ,连接
,连接![]() ,
, ![]() ,
,
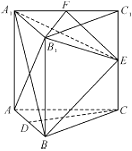
在三棱柱![]() 中,∵
中,∵![]() 平面
平面![]() ,
,
∴侧面![]() 底面
底面![]() ,
,
∵底面![]() 是正三角形,且
是正三角形,且![]() 是
是![]() 中点,∴
中点,∴![]() ,所以
,所以![]() 侧面
侧面![]() ,
,
∴![]() 是
是![]() 在平面
在平面![]() 上的射影.
上的射影.
∴![]() 是
是![]() 与平面
与平面![]() 所成角.
所成角.
![]() .
.


科目:高中数学 来源: 题型:
【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在![]() 岁的问卷中随机抽取了
岁的问卷中随机抽取了![]() 份, 统计结果如下面的图表所示.
份, 统计结果如下面的图表所示.
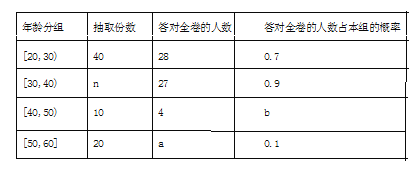
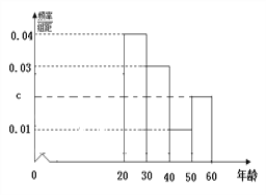
(1)分别求出![]() 的值;
的值;
(2)从年龄在![]() 答对全卷的人中随机抽取
答对全卷的人中随机抽取![]() 人授予“环保之星”,求年龄在
人授予“环保之星”,求年龄在![]() 的人中至少有
的人中至少有![]() 人被授予“环保之星”的概率.
人被授予“环保之星”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求实数k的值;
(2)设g(x)=log4(a2x+a),若f(x)=g(x)有且只有一个实数解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
平面直角坐标系中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知与直线![]() 平行的直线
平行的直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,试求
两点,试求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+c(a≠0),记f[2](x)=f(f(x)),例:f(x)=x2+1,
则f[2](x)=(f(x))2+1=(x2+1)2+1;
(1)f(x)=x2﹣x,解关于x的方程f[2](x)=x;
(2)记△=(b﹣1)2﹣4ac,若f[2](x)=x有四个不相等的实数根,求△的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是函数
是函数![]() 图象上的点,
图象上的点,![]() 是双曲线在第四象限这一分支上的动点,过点
是双曲线在第四象限这一分支上的动点,过点![]() 作直线,使其与双曲线
作直线,使其与双曲线![]() 只有一个公共点,且与
只有一个公共点,且与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,另一条直线
,另一条直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() .
.
则(1)![]() 为坐标原点,三角形
为坐标原点,三角形![]() 的面积为__________.
的面积为__________.
(2)四边形![]() 面积的最小值为__________.
面积的最小值为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com