
【题目】下列选项中说法正确的是( )
A.命题“p∨q为真”是命题“p∧q为真”的必要条件
B.向量 ![]() ,
, ![]() 满足
满足 ![]() ,则
,则 ![]() 与
与 ![]() 的夹角为锐角
的夹角为锐角
C.若am2≤bm2 , 则a≤b
D.“x0∈R,x02﹣x0≤0”的否定是“x∈R,x2﹣x≥0”
科目:高中数学 来源: 题型:
【题目】已知命题p:函数f(x)=(m2﹣1) ![]() 上为增函数;命题q:函数g(x)=x2﹣2elnx﹣m有零点.
上为增函数;命题q:函数g(x)=x2﹣2elnx﹣m有零点.
(I)若p∨q为假命题,求实数m的取值范围;
(Ⅱ)若p∨q为真命题,p∧q为假命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx﹣ ![]() )(ω>0)的图象与x轴的相邻两个交点的距离为
)(ω>0)的图象与x轴的相邻两个交点的距离为 ![]() .
.
(1)求w的值;
(2)设函数g(x)=f(x)+2cos2x﹣1,求g(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,AB= ![]() ,AF=1,G为线段AD上的任意一点.
,AF=1,G为线段AD上的任意一点. 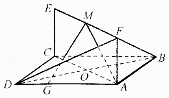
(1)若M是线段EF的中点,证明:平面AMG⊥平面BDF;
(2)若N为线段EF上任意一点,设直线AN与平面ABF,平面BDF所成角分别是α,β,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 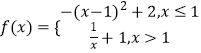 下列四个命题:
下列四个命题:
①f(f(1))>f(3); ② ![]() x0∈(1,+∞),f'(x0)=-1/3;
x0∈(1,+∞),f'(x0)=-1/3;
③f(x)的极大值点为x=1; ④ ![]() x1,x2∈(0,+∞),|f(x1)-f(x2)|≤1
x1,x2∈(0,+∞),|f(x1)-f(x2)|≤1
其中正确的有(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]()
![]() ,其中
,其中 ![]() =(2cosx,﹣
=(2cosx,﹣ ![]() sin2x),
sin2x), ![]() =(cosx,1),x∈R.
=(cosx,1),x∈R.
(1)求f(x)的单调递减区间;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,f(A)=﹣1,a= ![]() ,且向量
,且向量 ![]() =(3,sinB)与
=(3,sinB)与 ![]() =(2,sinC)共线,求边长b和c的值.
=(2,sinC)共线,求边长b和c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x﹣ ![]() )+2cos2x,将函数y=f(x)的图象向右平移
)+2cos2x,将函数y=f(x)的图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,则函数y=g(x)图象的一个对称中心是( )
个单位,得到函数y=g(x)的图象,则函数y=g(x)图象的一个对称中心是( )
A.(﹣ ![]() ,1)
,1)
B.(﹣ ![]() ,1)
,1)
C.( ![]() ,1)
,1)
D.( ![]() ,0)
,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程: ![]() (t为参数),曲线C的参数方程:
(t为参数),曲线C的参数方程: ![]() (α为参数),且直线交曲线C于A,B两点.
(α为参数),且直线交曲线C于A,B两点.
(Ⅰ)将曲线C的参数方程化为普通方程,并求θ= ![]() 时,|AB|的长度;
时,|AB|的长度;
(Ⅱ)已知点P:(1,0),求当直线倾斜角θ变化时,|PA||PB|的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +2x+sinx(x∈R),若函数y=f(x2+2)+f(﹣2x﹣m)只有一个零点,则函数g(x)=mx+
+2x+sinx(x∈R),若函数y=f(x2+2)+f(﹣2x﹣m)只有一个零点,则函数g(x)=mx+ ![]() (x>1)的最小值是 .
(x>1)的最小值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com