
【题目】如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,AB= ![]() ,AF=1,G为线段AD上的任意一点.
,AF=1,G为线段AD上的任意一点. 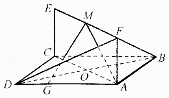
(1)若M是线段EF的中点,证明:平面AMG⊥平面BDF;
(2)若N为线段EF上任意一点,设直线AN与平面ABF,平面BDF所成角分别是α,β,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)证明:设AC∩BD=O,连结OF,OM,
由已知得AO=1,AF=1,
∴四边形AFMO是正方形,∴AM⊥OF,
又∵正方形ABCD和矩形ACEF所在平面互相垂直,交线是CA,DB⊥CA,
∴DB⊥平面ACEF,又AM平面ACEF,∴DB⊥AM,
∵BD∩OF=O,∴AM⊥平面BDF,
∵AM平面AMG,∴平面AMG⊥平面BDF
(2)解:∵正方形ABCD和矩形ACEF所在平面互相垂直,交线是CA,EC⊥CA,
∴EC⊥平面ABCD,∴CD、CB、CE两两垂直,
分别以CD、CB、CE为x,y,z轴建立坐标系,
则平面ABF的法向量 ![]() =(0,1,0),
=(0,1,0),
由(1)得平面BDF的法向量 ![]() =
= ![]() =(﹣
=(﹣ ![]() ,﹣
,﹣ ![]() ,1),
,1),
由N为线段EF上任意一点,
设 ![]() =
= ![]() =
= ![]() =λ(
=λ( ![]() ),(λ∈[0,1]),
),(λ∈[0,1]),
∴ ![]() =((λ﹣1)
=((λ﹣1) ![]() ,(λ﹣1)
,(λ﹣1) ![]() ,1),
,1),
∴sinα= 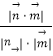 =
= ![]() =
= ![]() ,
,
∵λ∈[0,1],∴ ![]() =
= ![]() =1﹣
=1﹣ ![]() ∈[0,
∈[0, ![]() ].
].

【解析】(1)设AC∩BD=O,连结OF,OM,推导出AM⊥OF,DB⊥CA,从而DB⊥平面ACEF,进而DB⊥AM,AM⊥平面BDF,由此能证明平面AMG⊥平面BDF.(2)分别以CD、CB、CE为x,y,z轴建立坐标系,利用向量法能求出 ![]() 的取值范围.
的取值范围.
【考点精析】利用平面与平面垂直的判定对题目进行判断即可得到答案,需要熟知一个平面过另一个平面的垂线,则这两个平面垂直.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】已知 ![]() =(sinx,cos2x),
=(sinx,cos2x), ![]() =(
=( ![]() cosx,1),x∈R,设f(x)=
cosx,1),x∈R,设f(x)= ![]()
![]() .
.
(1)求f(x)的解析式及单调递增区间;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,且a=2,f(A)=1,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=eax﹣x. (Ⅰ)若曲线y=f(x)在(0,f(0))处的切线l与直线x+2y+3=0垂直,求a的值;
(Ⅱ)当a≠1时,求证:存在实数x0使f(x0)<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为非零实数,且对于任意的正整数n,都有(a1+a2+a3+…+an)2=a13+a23+a33+…+an3 .
(1)写出数列{an}的前三项a1 , a2 , a3(请写出所有可能的结果);
(2)是否存在满足条件的无穷数列{an},使得a2017=﹣2016?若存在,求出这样的无穷数列的一个通项公式;若不存在,说明理由;
(3)记an点所有取值构成的集合为An , 求集合An中所有元素之和(结论不要证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AA1=2,AB=BC=1,∠ABC=90°,外接球的球心为O,点E是侧棱BB1上的一个动点.有下列判断: ①直线AC与直线C1E是异面直线;②A1E一定不垂直于AC1;③三棱锥E﹣AA1O的体积为定值;④AE+EC1的最小值为2 ![]() .
.
其中正确的个数是( )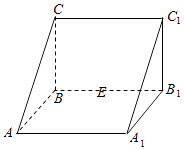
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的两个零点
的两个零点 ![]() 满足
满足 ![]() ,集合
,集合 ![]() ,则( )
,则( )
A.m∈A , 都有f(m+3)>0
B.m∈A , 都有f(m+3)<0
C.m0∈A , 使得f(m0+3)=0
D.m0∈A , 使得f(m0+3)<0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中说法正确的是( )
A.命题“p∨q为真”是命题“p∧q为真”的必要条件
B.向量 ![]() ,
, ![]() 满足
满足 ![]() ,则
,则 ![]() 与
与 ![]() 的夹角为锐角
的夹角为锐角
C.若am2≤bm2 , 则a≤b
D.“x0∈R,x02﹣x0≤0”的否定是“x∈R,x2﹣x≥0”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知椭圆 ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,C为椭圆上位于第一象限内的一点.
,C为椭圆上位于第一象限内的一点.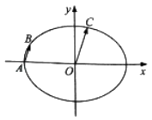
(1)若点C的坐标为(2, ![]() ),求a,b的值;
),求a,b的值;
(2)设A为椭圆的左顶点,B为椭圆上一点,且 ![]() =
= ![]() ,求直线AB的斜率.
,求直线AB的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com