
【题目】已知函数f(x)=|2x+![]() |+a|x﹣
|+a|x﹣![]() |.
|.
(Ⅰ)当a=﹣1时,解不等式f(x)≤3x;
(Ⅱ)当a=2时,若关于x的不等式2f(x)+1<|1﹣b|的解集为空集,求实数b的取值范围.
【答案】(1)![]() (2)[﹣7,9]
(2)[﹣7,9]
【解析】试题分析:
(1)零点分段可得不等式的解集为![]() ;
;
(2)利用绝对值不等式的性质,原问题转化为|1﹣b|≤8恒成立,据此可得实数b的取值范围是[﹣7,9].
试题解析:
解:(Ⅰ)当a=﹣1时,不等式f(x)=|2x+![]() |﹣|x﹣
|﹣|x﹣![]() |≤3x,
|≤3x,
等价于 ①;或
①;或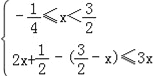 ②;或
②;或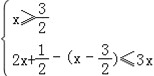 .
.
解①求得﹣![]() ≤x<﹣
≤x<﹣![]() ,解②求得﹣
,解②求得﹣![]() ≤x<
≤x<![]() ,解③求得x≥
,解③求得x≥![]() ,
,
故原不等式的解集为{x|x≥﹣![]() }.
}.
(Ⅱ)当a=2时,若关于x的不等式2f(x)+1<|1﹣b|,即 2(|2x+![]() |+2|x﹣|)+1<|1﹣b|,
|+2|x﹣|)+1<|1﹣b|,
即|4x+1|+|4x﹣6|+1<|1﹣b|.
由于|4x+1|+|4x﹣6|≥|(4x+1)﹣(4x﹣6)|=7,∴|1﹣b|>7+1的解集为,即|1﹣b|≤8恒成立,
∴﹣8≤b﹣1≤8,即﹣7≤b≤9,即要求的实数b的取值范围为[﹣7,9].


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.
(1) 求证:直线DE∥平面A1C1F;
(2) 求证:平面B1DE⊥平面A1C1F.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某集团公司为了获得更大的收益,决定以后每年投入一笔资金用于广告促销.经过市场调查,每年投入广告费t百万元,可增加销售额约(2t+ ![]() ﹣
﹣ ![]() )百万元(t≥0).
)百万元(t≥0).
(1)若公司当年新增收益不少于1.5百万元,求每年投放广告费至少多少百万元?
(2)现公司准备投入6百万元分别用于当年广告费和新产品开发,经预测,每投入新产品开发费x百万元,可增加销售额约( ![]() +3x+
+3x+ ![]() )百万元,问如何分配这笔资金,使该公司获得新增收益最大?(新增收益=新增销售额﹣投入)
)百万元,问如何分配这笔资金,使该公司获得新增收益最大?(新增收益=新增销售额﹣投入)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]()
![]() .
.
(Ⅰ)若直线![]()
![]() 与曲线
与曲线![]() 和
和![]() 分别交于
分别交于![]() 两点.设曲线
两点.设曲线
![]() 在点
在点![]() 处的切线为
处的切线为![]() ,
, ![]() 在点
在点![]() 处的切线为
处的切线为![]() .
.
(ⅰ)当![]() 时,若
时,若![]()
![]() ,求
,求![]() 的值;
的值;
(ⅱ)若![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅱ)设函数![]() 在其定义域内恰有两个不同的极值点
在其定义域内恰有两个不同的极值点![]() ,
, ![]() ,且
,且![]() .
.
若![]() ,且
,且![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的三个内角A,B,C所对的边,且满足(2b﹣a)cosC=ccosA.
(Ⅰ)求角C的大小;
(Ⅱ)设![]() ,求y的最大值并判断当y取得最大值时△ABC的形状.
,求y的最大值并判断当y取得最大值时△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学数学老师分别用两种不同教学方式对入学数学平均分和优秀率都相同的甲、乙两个高一新班(人数均为![]() 人)进行教学(两班的学生学习数学勤奋程度和自觉性一致),数学期终考试成绩茎叶图如下:
人)进行教学(两班的学生学习数学勤奋程度和自觉性一致),数学期终考试成绩茎叶图如下:
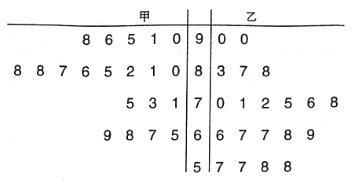
(1)现从乙班数学成绩不低于![]() 分的同学中随机抽取两名同学,求至少有一名成绩为
分的同学中随机抽取两名同学,求至少有一名成绩为![]() 分的同学被抽中的概率;
分的同学被抽中的概率;
(2)学校规定:成绩不低于![]() 分的优秀,请填写下面的
分的优秀,请填写下面的![]() 联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
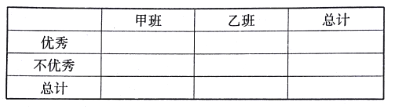
附:参考公式及数据

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为大力提倡“厉行节俭,反对浪费”,某高中通过随机询问100名性别不同的学生是否做到“光盘”行动,得到如表所示联表及附表:
做不到“光盘”行动 | 做到“光盘”行动 | |
男 | 45 | 10 |
女 | 30 | 15 |
P(K2≥k0) | 0.10 | 0.05 | 0.025 |
k0 | 2.706 | 3.841 | 5.024 |
经计算:K2= ![]() ≈3.03,参考附表,得到的正确结论是( )
≈3.03,参考附表,得到的正确结论是( )
A.有95%的把握认为“该学生能否做到光盘行到与性别有关”
B.有95%的把握认为“该学生能否做到光盘行到与性别无关”
C.有90%的把握认为“该学生能否做到光盘行到与性别有关”
D.有90%的把握认为“该学生能否做到光盘行到与性别无关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com