
【题目】如图,在直三棱柱ABC A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.
(1) 求证:直线DE∥平面A1C1F;
(2) 求证:平面B1DE⊥平面A1C1F.

【答案】(1)见解析(2)见解析
【解析】试题分析:(1)由三角形中位线性质及棱柱性质得DE∥A1C1,再根据线面平行判定定理得结论(2)先由直三棱柱性质得A1A⊥平面A1B1C1,即A1A⊥A1C1,又已知A1C1⊥A1B1,所以由线面垂直判定定理得A1C1⊥平面ABB1A1,即A1C1⊥B1D.再由已知B1D⊥A1F,结合线面垂直判定定理得B1D⊥平面A1C1F.最后根据面面垂直判定定理得平面B1DE⊥平面A1C1F.
试题解析:证明:(1)在直三棱柱ABC A1B1C1中,A1C1∥AC.
在△ABC中,∵D,E分别为AB,BC的中点,
∴DE∥AC,于是DE∥A1C1,
又∵DE平面A1C1F,A1C1平面A1C1F,
∴直线DE∥平面A1C1F.
(2)在直三棱柱ABC A1B1C1中,A1A⊥平面A1B1C1,
∵A1C1平面A1B1C1,∴A1A⊥A1C1,
又∵A1C1⊥A1B1,AA1平面ABB1A1,A1B1平面ABB1A1,A1A∩A1B1=A1,
∴A1C1⊥平面ABB1A1.
∵B1D平面ABB1A1,∴A1C1⊥B1D.
又∵B1D⊥A1F,A1C1平面A1C1F,A1F平面A1C1F,A1C1∩A1F=A1,
∴B1D⊥平面A1C1F.
∵B1D平面B1DE,∴平面B1DE⊥平面A1C1F.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人准备报考某大学,假设甲考上的概率为 ![]() ,甲,丙两都考不上的概率为
,甲,丙两都考不上的概率为 ![]() ,乙,丙两都考上的概率为
,乙,丙两都考上的概率为 ![]() ,且三人能否考上相互独立.
,且三人能否考上相互独立.
(1)求乙、丙两人各自考上的概率;
(2)设X表示甲、乙、丙三人中考上的人数与没考上的人数之差的绝对值,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x3+ax在(﹣1,0)上是增函数.
(1)求实数a的取值范围A;
(2)当a为A中最小值时,定义数列{an}满足:a1∈(﹣1,0),且2an+1=f(an),用数学归纳法证明an∈(﹣1,0),并判断an+1与an的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足:f′(x)>1﹣f(x),f(0)=3,f′(x)是f(x)的导函数,则不等式exf(x)>ex+2(其中e为自然对数的底数)的解集为( )
A.{x|x>0}
B.{x|x<0}
C.{x|x<﹣1或x>1}
D.{x|x<﹣1或0<x<1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 经过椭圆
经过椭圆![]()
![]() 的焦点.
的焦点.
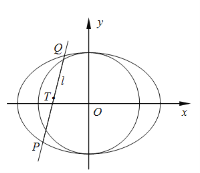
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点,![]() 为弦
为弦![]() 的中点,
的中点,![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为感谢全体员工的辛勤劳动,决定在年终答谢会上,通过摸球方式对全公司1000位员工进行现金抽奖。规定:每位员工从装有4个相同质地球的袋子中一次性随机摸出2个球,这4个球上分别标有数字![]() 、
、![]() 、
、![]() 、
、![]() ,摸出来的两个球上的数字之和为该员工所获的奖励额
,摸出来的两个球上的数字之和为该员工所获的奖励额![]() (单位:元)。公司拟定了以下三个数字方案:
(单位:元)。公司拟定了以下三个数字方案:
方案 |
|
|
|
|
一 | 100 | 100 | 100 | 500 |
二 | 100 | 100 | 500 | 500 |
三 | 200 | 200 | 400 | 400 |
(Ⅰ)如果采取方案一,求![]() 的概率;
的概率;
(Ⅱ)分别计算方案二、方案三的平均数![]() 和方差
和方差![]() ,如果要求员工所获的奖励额相对均衡,方案二和方案三选择哪个更好?
,如果要求员工所获的奖励额相对均衡,方案二和方案三选择哪个更好?
(Ⅲ)在投票选择方案二还是方案三时,公司按性别分层抽取100名员工进行统计,得到如下不完整的![]() 列联表。请将该表补充完整,并判断能否有90%的把握认为“选择方案二或方案三与性别有关”?
列联表。请将该表补充完整,并判断能否有90%的把握认为“选择方案二或方案三与性别有关”?
方案二 | 方案三 | 合计 | |
男性 | 12 | ||
女性 | 40 | ||
合计 | 82 | 100 |
附:![]()
| 0.15 | 0.10 | 0.05 |
| 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x+![]() |+a|x﹣
|+a|x﹣![]() |.
|.
(Ⅰ)当a=﹣1时,解不等式f(x)≤3x;
(Ⅱ)当a=2时,若关于x的不等式2f(x)+1<|1﹣b|的解集为空集,求实数b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com