
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 经过椭圆
经过椭圆![]()
![]() 的焦点.
的焦点.
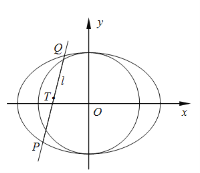
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点,![]() 为弦
为弦![]() 的中点,
的中点,![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)先确定交点位置:在![]() 轴上,再根据圆与
轴上,再根据圆与![]() 轴交点得等量关系:
轴交点得等量关系:![]() ;又
;又![]() ,所以
,所以![]() (Ⅱ)设
(Ⅱ)设![]() ,表示
,表示![]() ,然后根据直线与椭圆方程联立方程组,结合韦达定理表示中点
,然后根据直线与椭圆方程联立方程组,结合韦达定理表示中点![]() 坐标,并利用条件
坐标,并利用条件![]() 化简:
化简:![]() ,
,![]() ,最后代入并利用条件
,最后代入并利用条件![]() 化简得
化简得![]()
试题解析:解:(1)因![]() ,所以椭圆
,所以椭圆![]() 的焦点在
的焦点在![]() 轴上,
轴上,
又圆![]() 经过椭圆
经过椭圆![]() 的焦点,所以椭圆的半焦距
的焦点,所以椭圆的半焦距![]() , ……………3分
, ……………3分
所以![]() ,即
,即![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() . ……………6分
. ……………6分
(2)方法一:设![]() ,
,![]() ,
,![]() ,
,
联立 ,消去
,消去![]() ,得
,得![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]()
![]() ,
,
所以![]() ,
,![]() , ……………10分
, ……………10分
则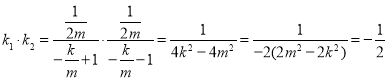 . …………14分
. …………14分
方法二:设![]() ,
,![]() ,
,![]() , 则
, 则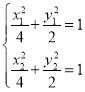 ,
,
两式作差,得![]() ,
,
又![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又![]() ,
,![]() 在直线
在直线![]() 上,∴
上,∴![]() ,∴
,∴![]() ,①
,①
又![]() 在直线
在直线![]() 上,∴
上,∴![]() ,②
,②
由①②可得![]() ,
,![]() . ……………10分
. ……………10分
以下同方法一.


科目:高中数学 来源: 题型:
【题目】下列各式中,所得数值最小的是( )
A.sin50°cos39°﹣sin40°cos51°
B.﹣2sin240°+1
C.2sin6°cos6°
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(sinx+ ![]() cosx)2﹣2.
cosx)2﹣2.
(1)当x∈[0, ![]() ]时,求函数f(x)的单调递增区间;
]时,求函数f(x)的单调递增区间;
(2)若x∈[﹣ ![]() ,
, ![]() ],求函数g(x)=
],求函数g(x)= ![]() f2(x)﹣f(x+
f2(x)﹣f(x+ ![]() )﹣1的值域.
)﹣1的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.
(1) 求证:直线DE∥平面A1C1F;
(2) 求证:平面B1DE⊥平面A1C1F.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长方体ABCD﹣A1B1C1D1中AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为( )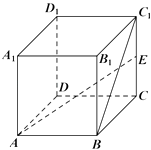
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是偶函数,且f(x+ ![]() )=f(
)=f( ![]() ﹣x),当﹣
﹣x),当﹣ ![]() ≤x≤0时,f(x)=(
≤x≤0时,f(x)=( ![]() )x﹣1,记an=f(
)x﹣1,记an=f( ![]() ),n∈N+ , 则a2046的值为( )
),n∈N+ , 则a2046的值为( )
A.1﹣ ![]()
B.1﹣ ![]()
C.![]() ﹣1
﹣1![]()
D.![]() ﹣1
﹣1![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com