
【题目】已知函数![]() .
.
(1)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(2)设函数![]() ,若
,若![]() 在
在![]() 上有两个不同极值点,求
上有两个不同极值点,求![]() 的取值范围,并判断极值的正负.
的取值范围,并判断极值的正负.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)把恒成立转化为![]() 在
在![]() 上恒成立。设函数
上恒成立。设函数![]() ,
, ![]() 求导求函数的最小值,只需
求导求函数的最小值,只需![]() 。(2)
。(2)![]() ,
, ![]() 转化为g(x)的导函数在
转化为g(x)的导函数在![]() 有奇次根。
有奇次根。![]() ,令
,令
![]() ,则
,则![]() .由
.由![]() ,得
,得![]() .结合函数图象可知,
.结合函数图象可知, ![]() 在
在![]() 上存在极值,分
上存在极值,分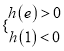 或
或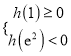 两种情况讨论。
两种情况讨论。
试题解析:(Ⅰ)由![]() ,得
,得![]() .
.
即![]() 在
在![]() 上恒成立.
上恒成立.
设函数![]() ,
, ![]() .
.
则![]() .
.
设![]() .
.
则![]() .易知当
.易知当![]() 时,
时, ![]() .
.
∴![]() 在
在![]() 上单调递增,且
上单调递增,且![]() .
.
即![]() 对
对![]() 恒成立.
恒成立.
∴![]() 在
在![]() 上单调递增.
上单调递增.
∴当![]() 时,
时, ![]() .
.
∴![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.
(Ⅱ)![]() ,
, ![]() .
.
∴![]()
![]() .
.
设![]() ,则
,则![]() .
.
由![]() ,得
,得![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
且![]() ,
, ![]() ,
, ![]() .
.
显然![]() .
.
结合函数图象可知,若![]() 在
在![]() 上存在极值,
上存在极值,
则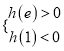 或
或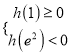 .
.
(ⅰ)当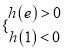 ,即
,即![]() 时,
时,
则必定![]() ,使得
,使得![]() ,且
,且![]() .
.
当![]() 变化时,
变化时, ![]() ,
, ![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
| - | 0 | + | 0 | - |
| - | 0 | + | 0 | - |
| ↘ | 极小值 | ↗ | 极大值 | ↘ |
∴当![]() 时,
时, ![]() 在
在![]() 上的极值为
上的极值为![]() ,且
,且![]() .
.
∵![]()
![]() .
.
设![]() ,其中
,其中![]() ,
, ![]() .
.
∵![]() ,∴
,∴![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
∵![]() ,∴
,∴![]() .
.
∴当![]() 时,
时, ![]() 在
在![]() 上的极值
上的极值![]() .
.
(ⅱ)当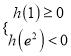 ,即
,即![]() 时,
时,
则必定![]() ,使得
,使得![]() .
.
易知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
此时, ![]() 在
在![]() 上的极大值是
上的极大值是![]() ,且
,且![]() .
.
∴当![]() 时,
时, ![]() 在
在![]() 上的极值为正数.
上的极值为正数.
综上所述:当![]() 时,
时, ![]() 在
在![]() 上存在极值,且极值都为正数.
上存在极值,且极值都为正数.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且 ![]() =2csinA
=2csinA
(1)确定角C的大小;
(2)若c= ![]() ,且△ABC的面积为
,且△ABC的面积为 ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.
(1) 求证:直线DE∥平面A1C1F;
(2) 求证:平面B1DE⊥平面A1C1F.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述正确的个数是( )
①若a>b,则ac2>bc2;
②若命题p为真命题题,命题q为假命题,则p∨q为假命题;
③若命题p:x0∈R,x ![]() ﹣x0+1≤0,则¬p:x∈R,x2﹣x+1>0.
﹣x0+1≤0,则¬p:x∈R,x2﹣x+1>0.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是偶函数,且f(x+ ![]() )=f(
)=f( ![]() ﹣x),当﹣
﹣x),当﹣ ![]() ≤x≤0时,f(x)=(
≤x≤0时,f(x)=( ![]() )x﹣1,记an=f(
)x﹣1,记an=f( ![]() ),n∈N+ , 则a2046的值为( )
),n∈N+ , 则a2046的值为( )
A.1﹣ ![]()
B.1﹣ ![]()
C.![]() ﹣1
﹣1![]()
D.![]() ﹣1
﹣1![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
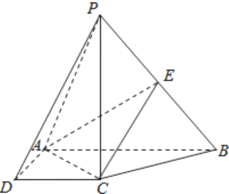
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() 是
是![]() 上的点.
上的点.
(1)求证: 平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,且二面角
的中点,且二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某集团公司为了获得更大的收益,决定以后每年投入一笔资金用于广告促销.经过市场调查,每年投入广告费t百万元,可增加销售额约(2t+ ![]() ﹣
﹣ ![]() )百万元(t≥0).
)百万元(t≥0).
(1)若公司当年新增收益不少于1.5百万元,求每年投放广告费至少多少百万元?
(2)现公司准备投入6百万元分别用于当年广告费和新产品开发,经预测,每投入新产品开发费x百万元,可增加销售额约( ![]() +3x+
+3x+ ![]() )百万元,问如何分配这笔资金,使该公司获得新增收益最大?(新增收益=新增销售额﹣投入)
)百万元,问如何分配这笔资金,使该公司获得新增收益最大?(新增收益=新增销售额﹣投入)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的三个内角A,B,C所对的边,且满足(2b﹣a)cosC=ccosA.
(Ⅰ)求角C的大小;
(Ⅱ)设![]() ,求y的最大值并判断当y取得最大值时△ABC的形状.
,求y的最大值并判断当y取得最大值时△ABC的形状.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com