
【题目】某公司为感谢全体员工的辛勤劳动,决定在年终答谢会上,通过摸球方式对全公司1000位员工进行现金抽奖。规定:每位员工从装有4个相同质地球的袋子中一次性随机摸出2个球,这4个球上分别标有数字![]() 、
、![]() 、
、![]() 、
、![]() ,摸出来的两个球上的数字之和为该员工所获的奖励额
,摸出来的两个球上的数字之和为该员工所获的奖励额![]() (单位:元)。公司拟定了以下三个数字方案:
(单位:元)。公司拟定了以下三个数字方案:
方案 |
|
|
|
|
一 | 100 | 100 | 100 | 500 |
二 | 100 | 100 | 500 | 500 |
三 | 200 | 200 | 400 | 400 |
(Ⅰ)如果采取方案一,求![]() 的概率;
的概率;
(Ⅱ)分别计算方案二、方案三的平均数![]() 和方差
和方差![]() ,如果要求员工所获的奖励额相对均衡,方案二和方案三选择哪个更好?
,如果要求员工所获的奖励额相对均衡,方案二和方案三选择哪个更好?
(Ⅲ)在投票选择方案二还是方案三时,公司按性别分层抽取100名员工进行统计,得到如下不完整的![]() 列联表。请将该表补充完整,并判断能否有90%的把握认为“选择方案二或方案三与性别有关”?
列联表。请将该表补充完整,并判断能否有90%的把握认为“选择方案二或方案三与性别有关”?
方案二 | 方案三 | 合计 | |
男性 | 12 | ||
女性 | 40 | ||
合计 | 82 | 100 |
附:![]()
| 0.15 | 0.10 | 0.05 |
| 2.072 | 2.706 | 3.841 |
【答案】(1)![]() (2)选择方案三较好(3)不能
(2)选择方案三较好(3)不能
【解析】试题分析:(Ⅰ)利用枚举法,写出所有的基本事件,找出其中方案一包含的基本事件上,再利用古典概型可求得概率;(Ⅱ)由已知数据,结合平均数与方差的的计算公式可求得结果;(Ⅲ)利用所给条件,填好列联表,求出常数![]() ,结合独立性检验及所给数据得出判断.
,结合独立性检验及所给数据得出判断.
试题解析:(Ⅰ)从a、b、c、d中取两个,共有ab、ac、ad、bc、bd、cd 这6个基本事件
采取方案一,设![]() 为事件A,它包含ab、ac、bc这3个基本事件
为事件A,它包含ab、ac、bc这3个基本事件
由于每个基本事件都是等可能的,所以![]()
(Ⅱ)依题意,求数据ab、ac、ad、bc、bd、cd的平均数![]() 和方差
和方差![]() 。
。
![]() ,
,
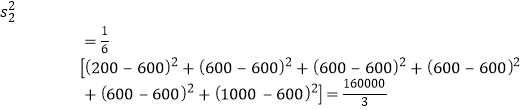 ,
,
![]() ,
,
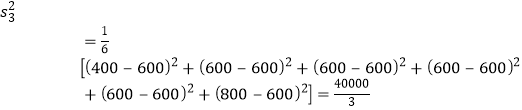 ,
,
![]() ,
,![]() ,方案三的方差较小,相对均衡,选择方案三较好。
,方案三的方差较小,相对均衡,选择方案三较好。
二 | 三 | 合计 | |
男性 | 12 | 48 | 60 |
女性 | 6 | 34 | 40 |
合计 | 18 | 82 | 100 |
(Ⅲ)
直接计算得,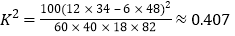 ,
,![]() ,
,
所以不能以![]() 的把握认为选择方案二或三与性别有关。
的把握认为选择方案二或三与性别有关。


科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)图象的一部分如图所示,函数g(x)=f(x+ ![]() ),则下列结论正确的是( )
),则下列结论正确的是( ) 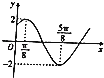
A.函数g(x)的奇函数
B.函数f(x)与g(x)的图象均关于直线x=﹣ ![]() π对称
π对称
C.函数f(x)与g(x)的图象均关于点(﹣ ![]() ,0)对称
,0)对称
D.函数f(x)与g(x)在区间(﹣ ![]() ,0)上均单调递增
,0)上均单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.
(1) 求证:直线DE∥平面A1C1F;
(2) 求证:平面B1DE⊥平面A1C1F.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是偶函数,且f(x+ ![]() )=f(
)=f( ![]() ﹣x),当﹣
﹣x),当﹣ ![]() ≤x≤0时,f(x)=(
≤x≤0时,f(x)=( ![]() )x﹣1,记an=f(
)x﹣1,记an=f( ![]() ),n∈N+ , 则a2046的值为( )
),n∈N+ , 则a2046的值为( )
A.1﹣ ![]()
B.1﹣ ![]()
C.![]() ﹣1
﹣1![]()
D.![]() ﹣1
﹣1![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
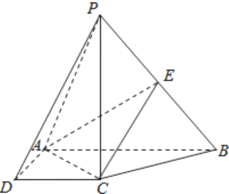
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() 是
是![]() 上的点.
上的点.
(1)求证: 平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,且二面角
的中点,且二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某集团公司为了获得更大的收益,决定以后每年投入一笔资金用于广告促销.经过市场调查,每年投入广告费t百万元,可增加销售额约(2t+ ![]() ﹣
﹣ ![]() )百万元(t≥0).
)百万元(t≥0).
(1)若公司当年新增收益不少于1.5百万元,求每年投放广告费至少多少百万元?
(2)现公司准备投入6百万元分别用于当年广告费和新产品开发,经预测,每投入新产品开发费x百万元,可增加销售额约( ![]() +3x+
+3x+ ![]() )百万元,问如何分配这笔资金,使该公司获得新增收益最大?(新增收益=新增销售额﹣投入)
)百万元,问如何分配这笔资金,使该公司获得新增收益最大?(新增收益=新增销售额﹣投入)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]()
![]() .
.
(Ⅰ)若直线![]()
![]() 与曲线
与曲线![]() 和
和![]() 分别交于
分别交于![]() 两点.设曲线
两点.设曲线
![]() 在点
在点![]() 处的切线为
处的切线为![]() ,
, ![]() 在点
在点![]() 处的切线为
处的切线为![]() .
.
(ⅰ)当![]() 时,若
时,若![]()
![]() ,求
,求![]() 的值;
的值;
(ⅱ)若![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅱ)设函数![]() 在其定义域内恰有两个不同的极值点
在其定义域内恰有两个不同的极值点![]() ,
, ![]() ,且
,且![]() .
.
若![]() ,且
,且![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学数学老师分别用两种不同教学方式对入学数学平均分和优秀率都相同的甲、乙两个高一新班(人数均为![]() 人)进行教学(两班的学生学习数学勤奋程度和自觉性一致),数学期终考试成绩茎叶图如下:
人)进行教学(两班的学生学习数学勤奋程度和自觉性一致),数学期终考试成绩茎叶图如下:
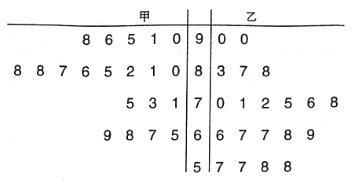
(1)现从乙班数学成绩不低于![]() 分的同学中随机抽取两名同学,求至少有一名成绩为
分的同学中随机抽取两名同学,求至少有一名成绩为![]() 分的同学被抽中的概率;
分的同学被抽中的概率;
(2)学校规定:成绩不低于![]() 分的优秀,请填写下面的
分的优秀,请填写下面的![]() 联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
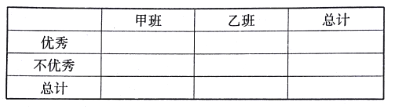
附:参考公式及数据

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com